Chapter 1: The Challenge Begins

In this article, we delve into an exciting challenge between myself and my students, one that has sparked numerous intriguing questions throughout the semester. This particular event occurred during the final week, and it was a thrilling competition of speed and knowledge.

The challenge unfolded as follows: - The students selected 20 math-related terms, including Integration, Complex Numbers, Trigonometry, and Exponents. These words were input into a random selection program, which ultimately determined that Exponents would be the theme for our challenge questions. - All student names were also entered into the program to select a quizmaster. Tasked with creating four relevant questions based on the theme of exponents, the quizmaster spent about 10 minutes preparing. - Once ready, the questions were projected for everyone to see, and the challenge commenced.

I'm pleased to share that I emerged victorious, albeit by a slim margin. I completed all four questions in roughly 1 minute and 53 seconds (113 seconds), while the top student finished in about 2 minutes and 13 seconds (133 seconds). Given my extensive experience, I was genuinely impressed by this student, along with others who finished closely behind.

I invite you to take on the challenge yourself. Dubbed the "133-Second Challenge" for fun, the focus here is not on speed but on accuracy. Below, I've included the questions as they were presented to us, along with various solving methods, including a more complex twist on one of the problems to keep things interesting. Good luck!

The questions were as follows: 1. Determine all values of a, b, c such that the ordered triplet (a, b, c) satisfies:

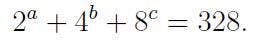
2. Find all values of m and n such that:

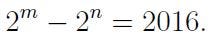
3. Solve for x such that:

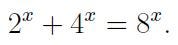
4. If

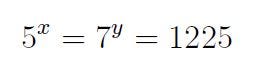
for x and y, find the value(s) of:

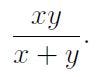
A Solution to Question 1

From the first question, we can conclude that a = 3, b = 2, and c = 1. Additionally, since:

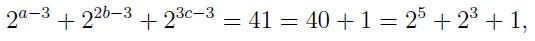
it follows that exactly one of a-3, 2b-3, or 3c-3 must equal zero, five, or three. We cannot have 2b-3=0 or 3c-3=5, leaving us with:

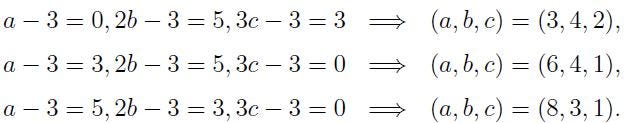
A Solution to Question 2

For the second question, we observe that:

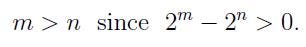
Thus, we can express that:

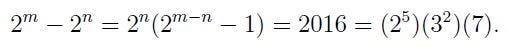
From this, we derive:

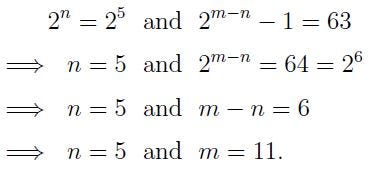
A Solution to Question 3

In addressing the third question:

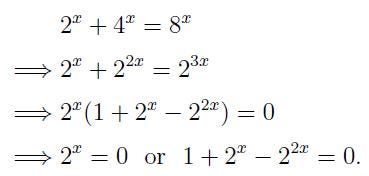
We might recognize this notable equation, or more crucially, its solutions, more easily using the substitution:

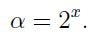
Using this substitution, we arrive at:

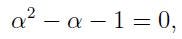
Thus, we find:

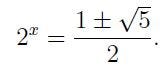
We can disregard the negative case, as it yields no real solution, and instead concentrate on:

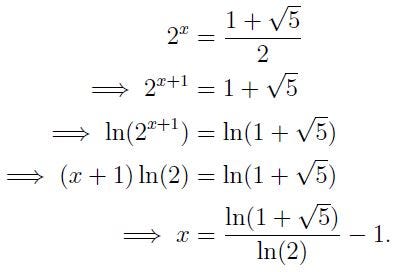
A Solution to Question 4

Considering the condition from the fourth question:

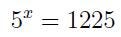
This leads to:

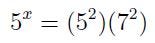
This is impossible for any values of x and y, indicating that we cannot find the values of:

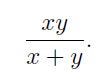
I suspect the student may have misrecorded the restrictions involving x and y. To extend the question, we can rephrase it for clarity: For x and y, determine the value(s) of:

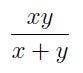
given that:

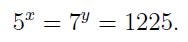
I will present two methods to solve this: the original approach I took and a more elegant method.

Method 1

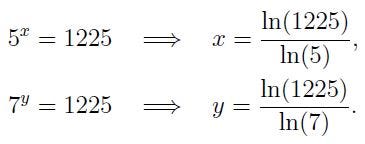
Thus,

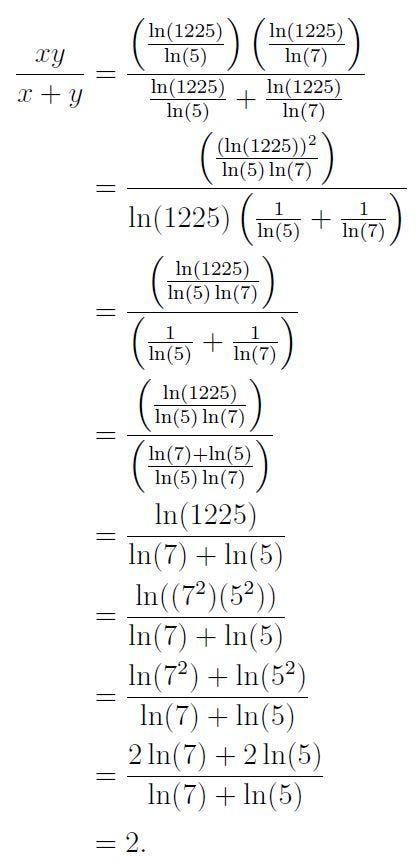
Method 2

Since neither x nor y can equal zero, we have:

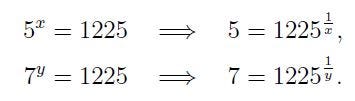
Now consider:

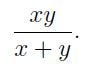
Experience indicates (and you can verify) that:

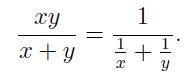
While we may not compute directly:

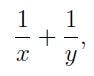
we can derive that:

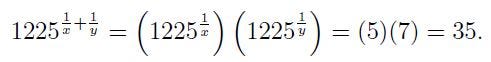
Thus, we find:

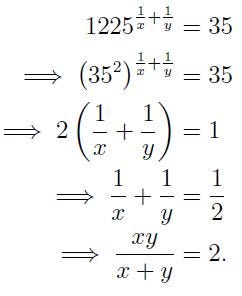
I hope you enjoyed this challenge! Feel free to share your results, and if anyone has alternative methods for tackling any of these problems, I’d love to hear them.

Thank you for reading. I encourage you to follow my work in Y(Math) so that my articles can reach a broader audience. If you're interested in contributing to Y(Math), please send a draft link to [email protected]. I would be delighted to welcome new writers!