Can You Solve This Challenging Logic Puzzle? Test Your Skills!
Written on
Chapter 1: Introduction to the Puzzle
Welcome back to another intriguing logic puzzle! This time, our beloved characters—Matt, Can, and Cheat—are returning to engage in a new challenge. For those unfamiliar with my earlier pieces, let me introduce our fictional trio: Matt is a human, Can is a playful puppy, and Cheat is a clever robot. As we embark on this puzzle, it's worth noting that, similar to the previous one, this puzzle leans towards the easier side as I continue to assess the format and audience engagement.
With that preliminary note out of the way, let's jump into the puzzle!
Section 1.1: The Puzzle Scenario
On a delightful sunny day, Matt, Can, and Cheat find themselves feeling a bit restless. While Can explores the yard, she stumbles upon a hidden treasure box. Excitedly, she calls over Matt and Cheat to share her discovery. They gather around as she opens the box, revealing three miniature toy versions of themselves. Naturally, they want to play with these newfound toys, but the question remains: who gets which toy?
The trio agrees that each will take one toy, and here’s what each has to say regarding the distribution:
Matt: “If I take Toy-Can, Cheat will take Toy-Matt.”
Can: “If I choose Toy-Cheat, Cheat will NOT take Toy-Matt.”
Cheat: “I’m NOT taking Toy-Can, and Matt won’t take Toy-Matt.”
Now, your challenge is to determine who ends up with which toy, keeping in mind that all three are truthful in their statements.
Spoiler Alert: If you want to attempt solving the puzzle first, I recommend pausing your reading here. Once you've given it a try, feel free to return for the solution.
Section 1.2: Approaching the Solution
In the initial installment of this logic puzzle series, I discussed two general methods for tackling such challenges:
- The top-down approach.
- The bottom-up approach.
The top-down strategy involves generalizing possibilities and eliminating them based on gathered information, while the bottom-up method entails accumulating information until a logical conclusion is reached. For this puzzle, I'll be employing both strategies concurrently, so don't worry if the theory seems tedious; we’ll dive into practical analysis shortly.
Gathering Information
The first critical point to recognize is that all three individuals are telling the truth, allowing us to logically evaluate their statements. Matt’s and Can's comments are conditional, indicating how Cheat will behave based on their choices, while Cheat’s statement provides direct information about his own choice and Matt’s.
Let’s analyze these statements more closely.
Subsection 1.2.1: Analyzing Cheat's Statement
Cheat's assertion is straightforward:
“I’m NOT taking Toy-Can, and Matt is NOT taking Toy-Matt.”
From this, we can derive two conclusions:
- Cheat cannot take Toy-Can, leaving him with Toy-Matt or Toy-Cheat.
- Matt cannot take Toy-Matt, so his options are limited to Toy-Can or Toy-Cheat.
By examining just one statement, we've already narrowed down the possibilities for both Cheat and Matt.
Subsection 1.2.2: Examining Can's Statement
Next, let’s consider Can's words:
“If I take Toy-Cheat, then Cheat cannot take Toy-Matt.”
This implies that if Can were to choose Toy-Cheat, Cheat would have no other toy available, leading us to conclude that Can did not take Toy-Cheat.
Subsection 1.2.3: Evaluating Matt's Statement
Finally, Matt states:
“If I take Toy-Can, then Cheat will take Toy-Matt.”
From this, we can infer that if Matt were to choose Toy-Can, Cheat would have to select Toy-Matt. However, since we already determined that Can did not take Toy-Cheat, it leads to a contradiction if Matt takes Toy-Can.
The Solution
Now that we’ve analyzed all the statements, let's solve the puzzle. Assuming Matt takes Toy-Can leads to the conclusion that Cheat must take Toy-Matt, which contradicts Can’s statement about not taking Toy-Cheat. Therefore, the only logical solution is that Matt must take Toy-Cheat.
This leaves Can and Cheat with the remaining toys: Toy-Matt and Toy-Can. Since Cheat cannot take Toy-Can, he must take Toy-Matt, leaving Can with Toy-Can.
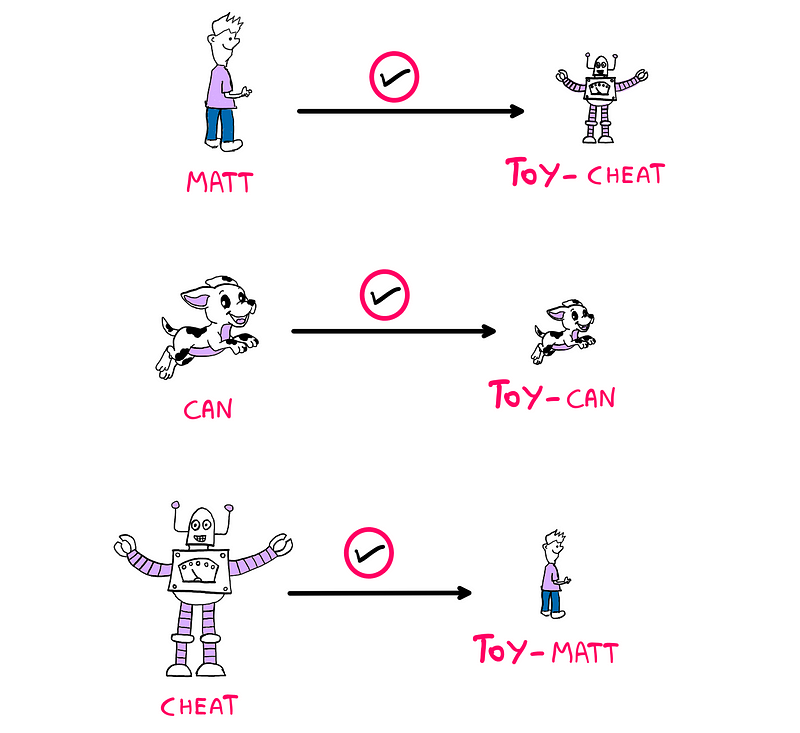
Thus, the final distribution is:
- Matt takes Toy-Cheat.
- Can takes Toy-Can.
- Cheat takes Toy-Matt.
Among the trio, Can is the happiest as she gets to play with her own toy version, perhaps a fitting reward from the treasure box for her keen eyes!
If you enjoy my work, consider supporting me by clapping, following, and subscribing.
Additional Reading:
- How To Solve The Monkey And The Coconuts Puzzle?
- How To Solve This Fun Geometry Puzzle?
- How To Tackle The Königsberg Bridge Problem?
For those interested in supporting future content, consider contributing on Patreon.