The Elegance of Euler’s Formula: Bridging Math, Physics, and Beyond
Written on
Euler’s formula, often referred to as Euler’s identity, stands out as one of the most remarkable equations in mathematics. Expressed as e^(i*pi) + 1 = 0, this equation encapsulates several vital mathematical principles and holds profound significance across various disciplines, including mathematics, physics, and artificial intelligence.
In machine learning, Euler’s formula is instrumental for the representation and manipulation of intricate data. It allows high-dimensional data to be expressed as complex numbers, streamlining data analysis and manipulation. This capability is particularly advantageous in unsupervised learning, aiding in data dimensionality reduction. Additionally, it plays a role in modeling neural networks, optimizing their dynamic behaviors and overall performance.
In the realm of natural language processing, Euler's formula aids in representing and processing textual information. It is utilized in sentiment analysis, enabling text data to be treated as complex functions and facilitating transformations such as rotation, scaling, and translation. This process enhances comprehension of text intent, emotion, and context.
The applications of Euler’s formula extend into computer vision, where it facilitates image representation as complex functions, enhancing image recognition and object detection capabilities.
Beyond these fields, Euler’s formula finds relevance in generative models, reinforcement learning, time series analysis, and the exploration of algorithms and computability.
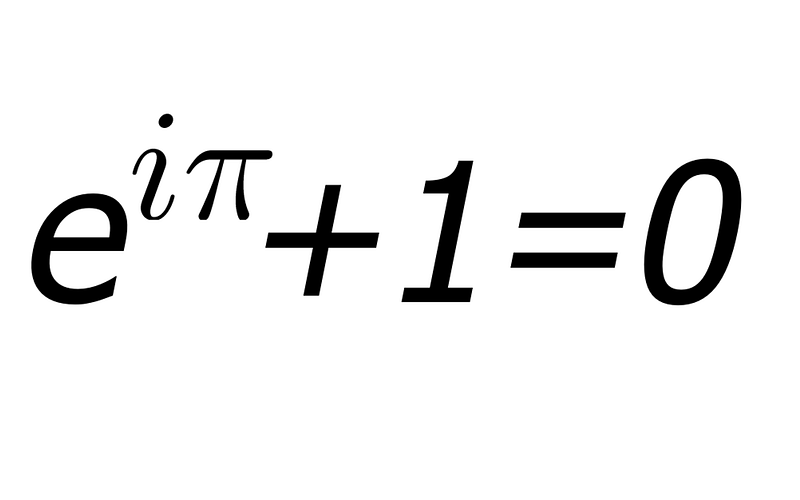
Named after Leonhard Euler, an influential Swiss mathematician of the 18th century, this formula reflects Euler’s numerous contributions to diverse mathematical fields, including calculus, trigonometry, and number theory. Notably, it connects five critical mathematical constants: e (the base of natural logarithms), i (the imaginary unit), pi (the ratio of a circle's circumference to its diameter), 0 (the additive identity), and 1 (the multiplicative identity).
The essence of Euler’s formula lies in complex numbers, which can be expressed as a + bi, where a and b are real numbers and i represents the imaginary unit, defined as the square root of -1. These complex numbers can be visualized on the complex plane, with the real part plotted on the x-axis and the imaginary part on the y-axis. Euler’s formula conveys that for any real number t, the following relation holds: e^(it) = cos(t) + i*sin(t).
This identity illustrates the relationship between trigonometric functions and complex numbers, bridging exponential functions with trigonometry, and has extensive implications in both mathematics and physics.
In mathematics, Euler’s formula simplifies the evaluation of complex integrals and assists in solving differential equations. In physics, it is significant in wave mechanics, appearing in the solutions to the Schrödinger equation, which describes quantum mechanical systems, and in studies involving electricity and magnetism.
Some have dubbed Euler’s formula “God’s Equation,” as it is seen as a representation of the universe's inherent unity and order, incorporating mathematical concepts from various branches, including algebra, trigonometry, calculus, and the complex plane, often linked with infinity.
The equation’s beauty also stems from its simplicity. Despite its ability to unify numerous critical mathematical concepts, it is expressed in a straightforward form that is accessible even to those unfamiliar with the technical intricacies of complex numbers or calculus. This simplicity makes it a popular introductory tool for teaching complex numbers and exponential functions.
Euler’s formula also intersects with various mathematical domains, such as group theory, number theory, and topology. In group theory, it defines the unitary operator, describing system symmetry. In number theory, it aids in determining the number of distinct solutions to specific equations known as Diophantine equations. In topology, it relates to the winding number of a closed curve in the complex plane.
Historically, Euler was not the first to encounter this formula; however, he was the first to publish it in its current form in a paper from 1748. Prior to him, mathematicians like De Moivre had employed similar formulas to express trigonometric functions via complex exponentials, but Euler was the first to articulate the relationship as the now-renowned equation.
Applications of Euler’s Formula
In signal processing, Euler’s formula is pivotal for representing and manipulating time-varying signals. For instance, it can express sinusoidal signals as complex exponentials, simplifying their analysis. In control systems, it allows engineers to model the dynamic behavior of systems, enabling precise tracking of desired trajectories.
In telecommunications, Euler’s formula aids in signal modulation representation and performance analysis of communication systems. It is instrumental in designing wireless communication systems, modeling signal propagation in the atmosphere, and optimizing overall system performance.
Moreover, it is applied in image and video processing, where it represents images as complex functions, facilitating transformations like rotation and scaling. In video processing, it models video as a sequence of images, enabling efficient compression for storage and transmission.
Euler’s formula also extends into computer science, influencing studies on algorithms, computability, and applications in computer-aided design, simulation, and modeling for time-dependent simulations.
Applications of Euler’s Formula in Artificial Intelligence
Within machine learning, Euler’s formula significantly contributes to representing and manipulating complex data. It simplifies high-dimensional data analysis by enabling representation as complex numbers, which is especially useful in unsupervised learning for dimensionality reduction. Additionally, it assists in modeling the dynamic behaviors of neural networks and optimizing their performance.
In natural language processing, Euler’s formula is valuable for text data representation and manipulation, particularly in sentiment analysis. It allows text to be viewed as a complex function, facilitating transformations that help decipher intent, emotion, and context.
The formula’s utility continues in computer vision, where it represents images as complex functions, enhancing recognition and detection tasks.
Beyond these applications, Euler’s formula is prevalent in generative models, reinforcement learning, and time series analysis.
Other Beautiful and Elegant Equations in Math and Physics
The mathematical landscape is rich with beautiful equations, each revealing unique aspects of the natural world and the universe’s structure. Here are a few notable examples:
- Pythagorean Theorem: a² + b² = c² illustrates the relationship between the sides of a right triangle, with numerous applications in mathematics and physics.
- The Gaussian Distribution: Also termed the normal distribution or bell curve, expressed as (1/(??(2?))) * e^(-(x-?)²/(2?²)), describes probability distributions of various natural phenomena.
- Schrödinger Equation: i?(d?/dt) = H? is foundational in quantum mechanics, detailing how a quantum system's wave function evolves over time.
- Navier-Stokes Equations: A set of equations governing fluid motion, integral to computational fluid dynamics simulations.
- The Wave Equation: d²y/dx² = (1/v²)(d²y/dt²) represents wave behaviors in mediums.
- Euler-Lagrange Equation: This equation determines a system's path requiring minimal energy, crucial in physics and engineering.
These equations are merely a glimpse into the vast array of beautiful mathematical expressions that enhance our understanding of the universe.
Books About Beautiful and Elegant Equations in Math and Physics
Here are several recommended books exploring elegant equations in mathematics and physics:
- “The Beauty of Fractals” by Heinz-Otto Peitgen and Peter Richter examines fractals, featuring stunning imagery and mathematical explanations.
- “The Elegant Universe” by Brian Greene presents string theory, providing a non-technical overview of its implications for our universe.
- “Einstein’s Equations” by Oliver Knill introduces general relativity's equations, discussing their mathematical basis and applications.
- “The Equations of Life” by Charles S. Cockell explores crucial equations in physics and chemistry related to life's origin and evolution.
- “The Art of Equation” by Ian Stewart analyzes beautiful equations and their connections to everyday life.
- “Beautiful Minds: The Parallel Lives of Great Apes and Dolphins” by Brian Hare and Vanessa Woods investigates behavior and cognition equations explaining evolutionary parallels.
Bio of Leonhard Euler
Leonhard Euler (1707–1783) was a prominent Swiss mathematician and physicist whose extensive contributions span various fields, including calculus, trigonometry, and number theory. Regarded as one of history's greatest mathematicians, his work remains integral to many scientific and engineering disciplines.
Born in Basel, Switzerland, in 1707, Euler began studying mathematics early and made significant contributions during his teens. He attended the University of Basel, working with Johann Bernoulli, a leading mathematician of his time. After graduation, Euler joined the St. Petersburg Academy of Sciences in Russia, where he spent over 25 years.
During his tenure at the academy, he published over 800 papers and books, including the seminal “Introduction to Analysis of the Infinite,” which offered a comprehensive overview of calculus and introduced the concept of mathematical functions. He also advanced number theory and introduced the Euler’s totient function, which calculates the number of integers less than a given integer that are coprime to it.
In addition to his mathematical and physical insights, Euler made significant contributions to astronomy and mechanics, applying calculus to planetary orbits and developing techniques still used in celestial mechanics.
Despite losing his eyesight in 1741, Euler continued producing an extraordinary volume of work, contributing over 800 papers and books, including “Letters to a German Princess,” a popularized mathematics textbook for the general public.
Euler passed away in 1783 in St. Petersburg, Russia, leaving behind a legacy recognized during his lifetime and continuing to influence modern mathematics. Many concepts and formulas, such as Euler’s formula, Euler’s number, and the Euler-Lagrange equation, bear his name.
> In summary, Euler’s formula is celebrated for its beauty, seamlessly connecting disparate mathematical concepts such as the exponential function, trigonometry, and complex numbers into a single cohesive equation. Its elegance, historical relevance, and broad applicability solidify its status as a mathematical masterpiece.