Chapter 1: The Allure of Tetris

Tetris stands as one of the most beloved video games ever created, having enchanted players globally since its launch in 1984. What many may not realize is that Tetris transcends mere entertainment; it serves as an intriguing subject for mathematical exploration. Central to Tetris is the idea of polyominoes—geometric configurations made up of interconnected squares. In this discussion, we will delve into the mathematics surrounding polyominoes and their relevance to Tetris.

To begin, we will clarify what polyominoes are and outline their characteristics. Following that, we will examine how they are analyzed within the realm of mathematics, consider various types of polyominoes, and discuss their applications, including their role in Tetris. Finally, we will highlight the significance of understanding polyominoes in everyday contexts and encourage further investigation into this captivating area of mathematics.

What Exactly Are Polyominoes?

Polyominoes consist of connected squares, formed by linking a finite number of squares edge-to-edge. Each square is referred to as a “cell” or “unit square,” and all cells are regarded as identical.

Here are some examples of polyominoes:

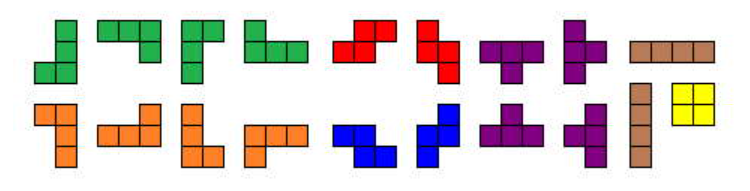
Polyominoes can be categorized based on their shape and size. An “n-omino” is the term used for a polyomino comprising n cells. The simplest form, known as the monomino, consists of just a single square, while the domino, made up of two squares, is the next simplest variant. The figure below illustrates the initial examples of polyominoes:

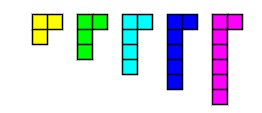
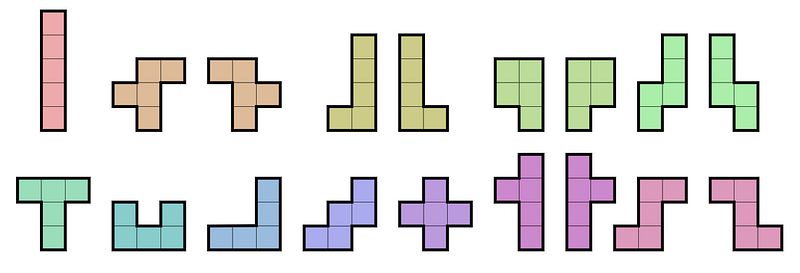
Polyominoes exhibit numerous intriguing characteristics. They can be reflected and rotated like any other geometric figure, although not every reflection or rotation produces a new polyomino. Moreover, the count of distinct n-ominoes increases rapidly as n grows. For instance, while there are only two unique trominoes (three-cell polyominoes), there are 35 distinct hexominoes (five-cell polyominoes). Below are all 18 unique pentominoes:

Polyominoes hold significant value in mathematics, as they can model various real-world scenarios, such as surface tiling and protein folding. In the following section, we will delve deeper into the mathematical properties of polyominoes.

Polyominoes in Mathematical Study

The extensive study of polyominoes in mathematics stems from their captivating properties and diverse applications. Here, we will discuss some mathematical aspects of polyominoes.

A key challenge in polyomino theory is determining the count of polyominoes of a specific size. Given a positive integer n, how many distinct polyominoes exist with n cells? This inquiry becomes increasingly complex as n increases, leading to an exponential growth in the number of distinct polyominoes.

To illustrate, there are five distinct tetrominoes, twelve distinct pentominoes, and 35 distinct hexominoes. Once we reach nononinos (comprising nine cells), the count surpasses 1000!

Despite the complexity of this challenge, numerous mathematicians have explored it, uncovering intriguing patterns and formulas. For instance, the distinct n-ominoes are represented by a series of values known as “polyomino numbers.” These have been studied extensively and linked to other mathematical fields like combinatorics and number theory.

Polyominoes can also be utilized for tiling surfaces, which is crucial in fields such as computer science and materials science. Tiling refers to covering a surface entirely with non-overlapping copies of a specific tile.

Researching polyomino tilings remains an active mathematical domain. Notably, while some polyominoes can successfully tile a rectangle, others can only tile different shapes like triangles or hexagons.

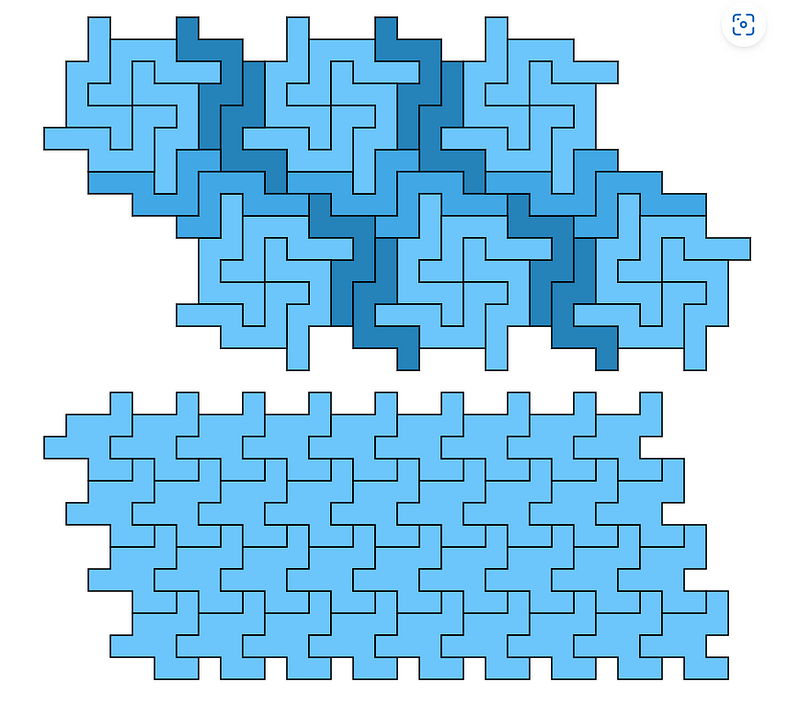
The applications of polyomino tilings extend to computer science, where they help devise algorithms for efficiently packing shapes into confined spaces, such as optimizing box arrangements within shipping containers.

Polyominoes also possess many other fascinating mathematical properties, including their symmetry, connectivity, and potential to create fractals. These properties are valuable in various scientific fields, including physics, chemistry, and biology. Fractals—complex geometric patterns exhibiting self-similarity across different scales—are prevalent in nature, from the branching of trees to the irregular contours of coastlines.

One method of creating a fractal using polyominoes is through iteration. Starting with a basic polyomino, like a square or rectangle, we can repeatedly apply specific transformation rules to generate more complex shapes. For example, substituting each cell in the polyomino with a larger polyomino of a certain shape allows us to create intricate designs over successive iterations.

As this process continues, the resulting shape becomes increasingly intricate, demonstrating self-similarity at various scales. Fractals constructed from polyominoes find applications in computer graphics and digital signal processing, as well as in physics for modeling complex system behaviors, such as fluid dynamics or crystal growth.

Additionally, the aesthetic appeal of fractals has led to their use in art and design. The unique, self-similar patterns formed by fractals can create stunning and detailed designs, as seen in Islamic art and architecture.

Conclusion

Polyominoes are captivating geometric figures with numerous applications in mathematics and daily life. They serve as the foundation for the popular game Tetris, which has fascinated millions globally. By comprehending the properties of polyominoes, we can better understand the intricate behaviors of systems comprised of numerous interconnected components. Whether you're a devoted Tetris enthusiast or simply curious about the world of mathematics, polyominoes are a topic that is bound to intrigue and inspire.

In the first video, "Fun with Polyominoes | Elementary Mathematics (K-6) Explained 6 | NJ Wildberger," the speaker introduces the concept of polyominoes in a fun and engaging manner, making the topic accessible to younger audiences.

The second video, "The Pentomino Puzzle (and Tetris) - Numberphile - YouTube," explores the relationships between pentominoes and Tetris, delving into the puzzles and challenges they present.