Chapter 1: Introduction to Polynomials

Polynomials have been an essential part of mathematics for centuries. Did you know that in 1676, polynomials were instrumental in calculating the speed of light? This mathematical structure has been utilized since ancient times, helping us interpret the world and solve intricate equations.

A polynomial consists of variables, coefficients, and constants, allowing us to describe various relationships and patterns. They serve as foundational elements in mathematics education, equipping students with the necessary skills to tackle advanced subjects like calculus. Additionally, polynomials are crucial in various sectors, including business and engineering, where they aid in data analysis, outcome prediction, and informed decision-making.

Chapter 2: The Historical Development of Polynomials

In this section, we will delve into the historical evolution of polynomials, examining their diverse forms, real-world applications, and the challenges that arise when working with them.

The term "polynomial" was first recorded in 1637 when René Descartes published La Géométrie. In this work, he referred to equations with multiple variables derived from powers and constants. Over the years, many mathematicians, including Leonhard Euler and Joseph-Louis Lagrange, have significantly advanced our understanding of polynomials.

This rich history contributes to our current knowledge, enabling us to solve increasingly complex equations.

Section 2.1: Types of Polynomial Expressions

Polynomials exist in various forms, each with unique characteristics and applications.

Linear equations, represented as ax + b = c, consist of two variables and are essential for modeling straight-line relationships, such as price versus quantity.

Quadratic equations feature three terms—one coefficient (ax²), one linear term (bx), and one constant (c). These equations help us understand curves and can be used to find maximum or minimum values on a graph. More complex forms include cubic equations (ax³ + bx² + cx + d) and quartic equations (ax⁴ + bx³ + cx² + dx + e).

These diverse forms allow for better analysis of complex datasets, enhancing decision-making based on factual information. For example, cubic equations can forecast stock market trends, while quartic expressions can optimize aircraft flight paths.

This engaging video titled "A Fun Problem With Polynomials" illustrates how polynomials can be applied to solve interesting mathematical challenges.

Section 2.2: Solving Polynomial Equations

Understanding variables and coefficients is crucial in solving polynomial equations. For example, in a simple linear equation like 2x + 7 = 0, "x" is the variable and "2" is the coefficient. By isolating the variable, we find the solution x = -3.5.

In contrast, quadratic equations require more intricate manipulation. For instance, to solve x² + 5x - 3 = 0, we apply the quadratic formula:

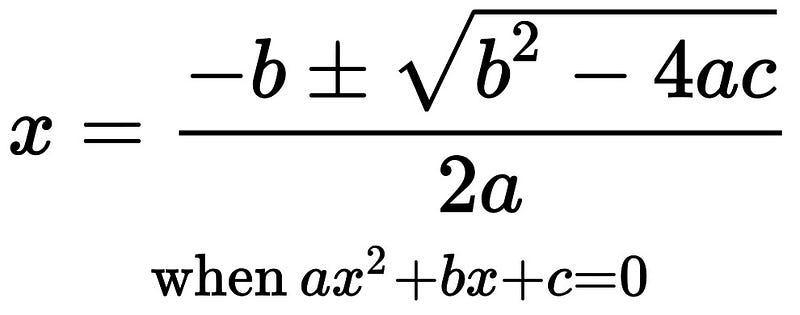
This process highlights the necessity of understanding how variables and coefficients interact.

The video "How to Solve this Polynomial Equation - Increase your Algebra Skills" provides insights into solving polynomial equations effectively, enhancing your algebra skills.

Chapter 3: Real-World Applications of Polynomials

Polynomials play a pivotal role in mathematics education, helping students grasp basic algebraic concepts. This foundational knowledge is vital as they face more complex mathematical challenges in the future.

In the business world, polynomials are frequently utilized in accounting, economic forecasting, and stock market analysis. By manipulating data through equations, businesses gain insights into future trends based on current conditions.

Engineers also depend on polynomials for construction and robotics. Identifying patterns in equations allows them to create models that accurately reflect reality. Aerospace engineering, in particular, relies heavily on polynomials to design vehicles capable of enduring the rigors of space travel.

Chapter 4: Challenges in Working with Polynomials

Despite their utility, working with polynomial expressions can be challenging. Mathematicians often encounter difficulties when dealing with irrational, imaginary, or complex numbers, which require unique techniques for manipulation.

Additionally, differentiating between upper and lower terms while solving equations can complicate the process. Failing to simplify terms in the correct order may lead to incorrect results.

Moreover, some expressions may lack common factors, presenting additional obstacles in factoring.

In conclusion, polynomials have a long-standing presence in mathematics and continue to be integral in various fields today. Understanding their significance and challenges equips us for success in careers that involve mathematical applications. Therefore, it is essential to appreciate the importance of polynomials in our daily lives and pursue further knowledge on this intriguing subject.

If you found this exploration of polynomials enlightening, consider joining the Medium community for exclusive content on mathematics and beyond! Your support helps writers continue creating engaging articles.