Innovative Numerical Integration Through Differentiation Methods
Written on
Chapter 1: Understanding Integration and Differentiation
In high school, we learn that integration is essentially the reverse of differentiation, which is a correct perspective. However, there's a less commonly acknowledged fact: integration can also be achieved through differentiation. This article will provide a numerical perspective on this concept. We'll introduce a method that not only exceeds traditional integration techniques but also adapts to higher-order methods and various grid types.
Daily Dose of Scientific Python
Solving both common and complex problems using Numpy, Sympy, SciPy, and matplotlib.
The Concept
We begin by defining an integral:
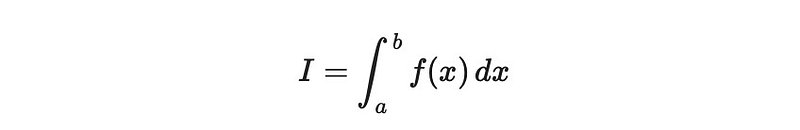
To keep the upper limit of integration variable, we present:
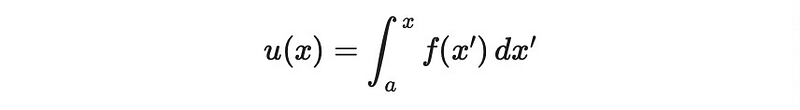
From this, we can express:
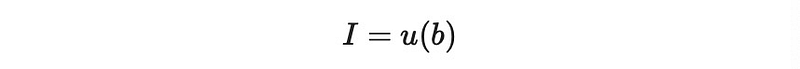
Taking the derivative yields:
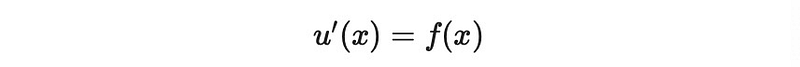
This results in a differential equation for the function u(x). Hence, determining the integral equates to solving this differential equation under specified boundary conditions.
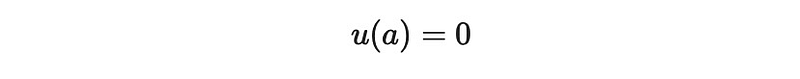
We can reformulate the differential equation with alternative notation, guiding us toward our next steps:
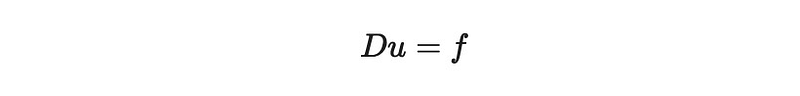
So far, we've avoided approximations, maintaining a continuous framework. However, numerical methods require us to discretize our functions and operators. Thus, functions transform into vectors, and operators into matrices. This leads us to the following discretized equation:
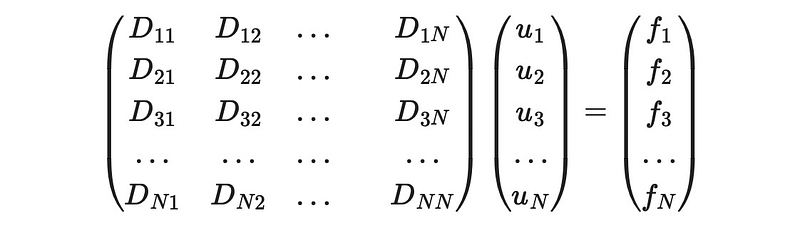
The fundamental idea is to multiply by the inverse matrix to obtain our solution function u. To implement the boundary condition u(a)=0, we need to adjust our equation system accordingly. This results in:
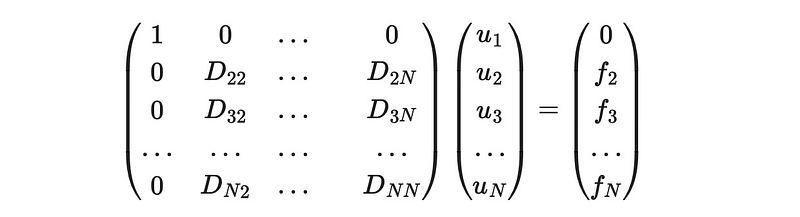
This adjustment effectively removes the first row and column while ensuring the diagonal entry is set to 1. Additionally, on the right side, we replace f_1 with 0, satisfying both conditions: enforcing u_1=0 and informing other equations of this condition.
However, we can simplify further by eliminating the submatrix, leading us to:
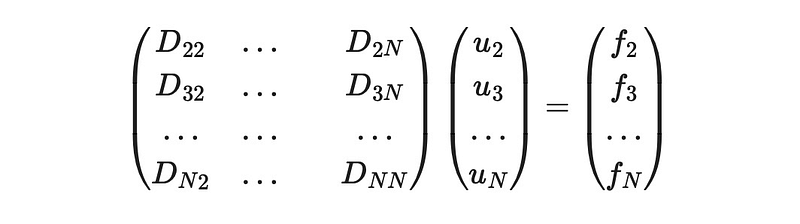
Let's denote these smaller components with a tilde. Inverting this yields:
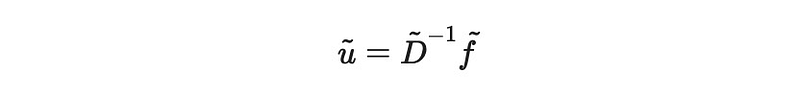
Python Implementation
Having explored the theoretical foundations of integrating through differentiation, let’s implement this concept in Python. We will integrate the function f(x) = cos x from -1 to 1, allowing us to compare our result with the exact integral value of ∫ f(x) dx = sin(1) - sin(-1).
We will utilize an equidistant grid for simplicity:

Next, we need a matrix representation of a differential operator. For simplicity, we will use finite difference approximations, which are applicable to various other approximations as well. Regardless of the approximation method, a matrix representation of the derivative operator is essential.
In Python, the findiff package provides a straightforward way to achieve finite difference approximations. I previously wrote an introductory article on its application.
As shown, findiff produces a sparse matrix representation, which is advantageous since finite difference matrices typically contain many zeros.
Now, let’s focus on the lower section of our matrix and vectors:
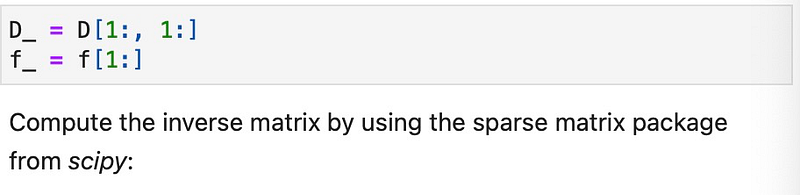
We can eliminate the last row of the inverse matrix:

Then, we perform a dot multiplication with our function vector:

The result is produced! The error calculation is as follows:

While the error is acceptable, there's room for improvement. By default, findiff provides a second-order accuracy approximation for the matrix D. However, we can achieve higher accuracy by simply adjusting a parameter:

This improvement significantly enhances accuracy! When compared to traditional integration techniques, this method transitions from a second-order approach to a fourth-order one, similar to progressing from the trapezoidal rule to Simpson's rule. Importantly, our method is adaptable to any grid size, unlike Simpson's rule, which is limited to even numbers of grid points.
Conclusion
The method of numerical integration through differentiation has yielded fascinating outcomes. Our Python implementation effectively illustrated the method's capabilities and flexibility, demonstrating its generalizability to higher-order techniques regardless of grid configurations. In contrast to conventional integration methods, this approach excels due to its adaptability to various grid sizes, addressing a common limitation found in techniques like Simpson’s rule.