Chapter 1: Introduction to Quantum Operators

If you've been exploring the fundamental principles of quantum physics, you may have encountered the term "operators." When I first delved into quantum mechanics, I found the concept quite bewildering. Many explanations regarding what an "operator" truly is often left me more confused, as they sometimes contradicted each other. It's safe to say that the topic of operators is frequently inadequately addressed, even in academic textbooks. The purpose of this article is to clarify the essence of quantum operators.

An operator functions by acting on an eigenfunction, producing an output that is the corresponding eigenvalue multiplied by that same eigenfunction. Sounds complex, right? Let's break this down. We need to understand three key terms: eigenfunction, eigenvalue, and operator. To grasp these concepts, a brief review of linear algebra is essential.

In linear algebra, we learn that matrices operate on vectors, generating new vectors, similar to how functions manipulate scalars to yield new scalars. Here’s an illustrative example.

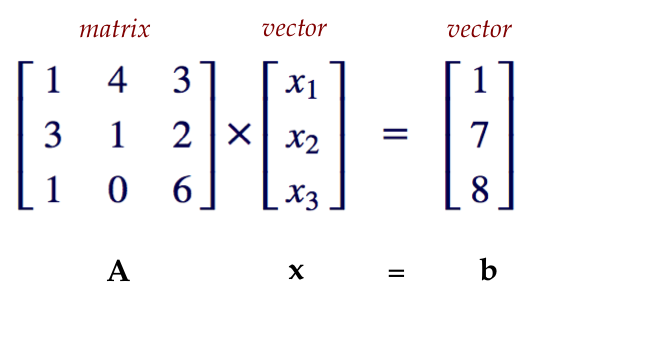
Consider matrix A acting on vector x to produce vector b. What does this signify visually?

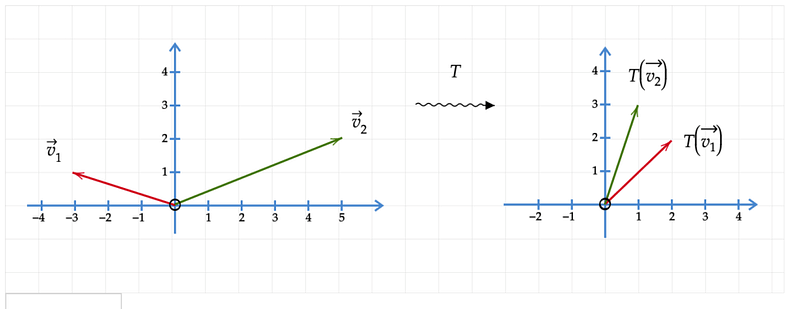
This illustrates that the matrix transforms one vector by scaling and rotating it to create a new vector. Essentially, matrices represent linear transformations. Focusing on one colored arrow in the image above, we see that matrix T alters vector #2 by scaling and rotating it. When observing both sets of vectors, it's evident that the same matrix treats each vector differently; for example, it rotates vector #1 significantly but only scales it slightly, while for vector #2, it rotates it minimally but significantly alters its length. This should clarify that a matrix's action varies across different initial vectors.

Although this review of linear algebra may seem tangential, it is indeed relevant. Now, let's define an eigenvector: it is a vector that, when a matrix acts on it, is scaled by a specific factor known as the eigenvalue. In mathematical terms, this can be expressed as: If M(v) = av, then v is the eigenvector and a is the eigenvalue.

From the illustration above, we see that vector x has been scaled by a specific factor after the action of matrix A, without any rotation. Hence, vector x is the eigenvector corresponding to matrix A, and lambda represents the eigenvalue associated with vector x.

Now, returning to our original definition, we see an intriguing connection: "An operator acts on an eigenfunction, yielding an output of the eigenvalue multiplied by that eigenfunction." And in the case of eigenvectors, they are defined as vectors that, when acted upon by a matrix, are only scaled by a specific amount—the eigenvalue.

This correlation is not coincidental; an eigenfunction is essentially an eigenvector but for functions. What acts on eigenvectors? Matrices! Thus, an operator is a linear map that operates on a function and returns a scalar value multiplied by that same function, provided that function is an eigenfunction.

Let's place this in the context of quantum mechanics. The Q operator acts on an eigenfunction A, returning the same eigenfunction A multiplied by an eigenvalue q, where q denotes an observable quantity. For instance, the position operator acts on the wave function, yielding the same wave function multiplied by the position eigenvalue, which signifies the definite position of a particle. Similarly, the momentum operator acts on the wave function, yielding the same wave function multiplied by the particle's definite momentum.

The energy operator (also known as the Hamiltonian) functions similarly, acting on the wave function and returning it multiplied by the particle's definite energy. Notably, not all wave functions satisfy the "eigenvalue problem," which is the term for these equations. The wave functions that do satisfy these equations (aside from the Hamiltonian) are termed eigenfunction wave functions. This may seem circular, but it is accurate: the eigenvalue problem holds true for eigenfunctions, which are defined as functions that meet the eigenvalue problem's criteria. In essence, the eigenvalue problem applies only when it is applicable, and when it is, the function in question is an eigenfunction.

It's important to note that no realistic particles can be described solely by eigenfunctions (except for the Hamiltonian), as this would imply absolute certainty regarding a particle's momentum, position, and other properties—something that contradicts the Heisenberg uncertainty principle (as discussed in my previous post).

You might think that eigenfunctions are somewhat futile since they don't accurately depict real states. However, there is hope, as a superposition of eigenfunctions can indeed represent real states. Take, for instance, the free particle potential. The wave function for a free particle is expressed as e^(-ikx+vt), where k is the quantum state and v represents the wave's velocity. This equation describes a plane wave, and when multiplied by the momentum operator, it results in a real constant multiplied by the same wave function (that constant being hk). Though the wave function for individual free particle states are eigenfunctions, they cannot accurately represent real particles. Nevertheless, a superposition of all possible states can yield a non-eigenfunction that adheres to the uncertainty principle. This function will neither be completely spread across momentum space nor be sharply peaked in position space. We won’t delve into the mathematics of this, but it's a compelling example showing how superpositions of non-real states can yield real states.

If you've been attentive, you may have realized that the renowned Schrödinger Equation is fundamentally an eigenvalue problem.

We will explore this equation further in future discussions. It's fascinating how concepts from linear algebra seamlessly integrate into quantum physics.

Chapter 2: Exploring Quantum Operators in Depth

In this first video, "Operators in Quantum Mechanics," the presenter explains the essential role of operators in quantum mechanics, detailing how they function and their significance in the field.

The second video, "Ever Heard of Quantum Operators and Commutators? (Explained for Beginners)," offers an accessible introduction to quantum operators and their relationship with commutators, ideal for those new to the subject.