Chapter 1: What is Time Complexity?

Time complexity is an essential concept in computer science that measures how the execution time of an algorithm changes with varying input sizes. Let's consider a scenario where you are looking for the number 1024 within a series of numbers:

There are various approaches to locate 1024. One method is to begin with the first number, 1, and sequentially check each element until you reach 1024, after examining 32 numbers.

This linear approach is quite slow. Instead, you might opt to jump forward five elements at a time. Using this method, you would check numbers like 25, 100, 225, and so on, before backtracking to find 1024.

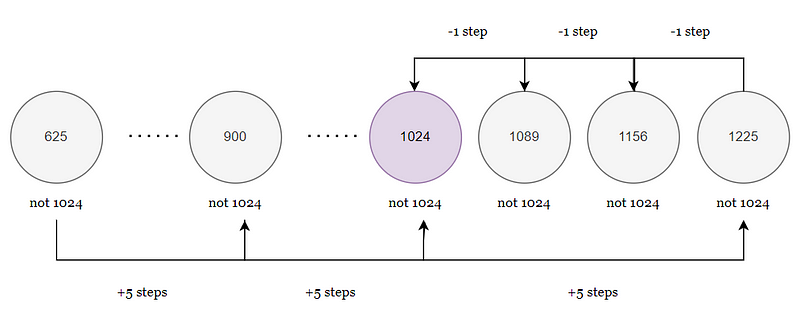
In total, you would have examined 10 elements using this strategy—better than 32, but still not optimal. A more efficient method involves starting from the middle of the list, repeatedly halving it until reaching 1024.

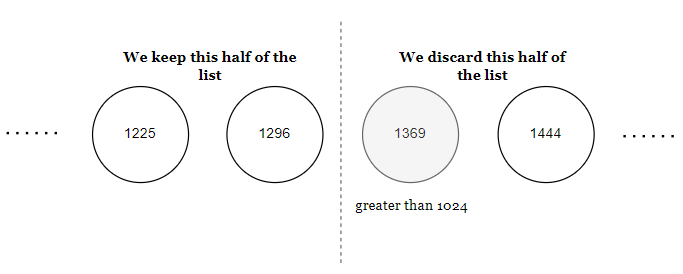
By continually halving the list, you can locate 1024 much faster than with the previous methods. Interestingly, if you recognize that the first element represents the first square, the second the second square, and so forth, you can pinpoint 1024 in a single step since it is the square of 32.

This example illustrates four different searching algorithms, each with varying execution times, introducing the concept of time complexity.

Chapter 2: Big O Notation Explained

Big O notation is a mathematical representation used to describe the upper limit of an algorithm's time complexity. It allows us to express how the execution time of an algorithm relates to the size of its input, denoted as n.

To summarize the key aspects of Big O notation, consider the following table:

Let's evaluate the time complexity of the previously mentioned algorithms. The last method we discussed—finding the square root of a number—involves just one step, regardless of the list size. Thus, its time complexity is classified as O(1).

Conversely, the linear search algorithm would require a maximum of 72 steps for a list containing 72 elements, making its time complexity O(n). Although the second approach took fewer steps, it also scales linearly with n, thus also having a time complexity of O(n).

The third method, which involved halving the list, results in a logarithmic time complexity of O(log(n)), as the size of the list diminishes exponentially with each comparison.

Summary

Understanding the time complexity of an algorithm is crucial in evaluating its efficiency. Big O notation provides a framework for expressing this time complexity concerning the input size, n.

Thank you for reading! If you're interested in exploring additional fundamental computer science concepts, check out the links below.

Introduction to Object Oriented Programming in Python

The Beginner's Guide to Objects and Classes

code.likeagirl.io

Error Correction Demystified

Your guide to the intuition behind error correction.

More content at plainenglish.io. Sign up for our free weekly newsletter. Get exclusive access to writing opportunities and advice in our community Discord.