Well-Posedness

At its core, a differential equation consists of a function and its derivatives. Unlike algebraic equations, where solutions are typically numerical, solutions to differential equations are functions. If the function ( u ) has one independent variable, its domain ( D ) is a subset of real numbers, categorizing it as an ordinary differential equation (ODE). Conversely, if ( u ) has ( n ) independent variables, it becomes a partial differential equation (PDE).

A differential equation problem is deemed well-posed if:

1. A solution exists.
2. The solution is unique.
3. The solution varies continuously with changes in input data.

Let’s expand on these conditions. The first condition is rather straightforward; it simply indicates that there are formulations of differential equations that may not yield any solutions. Naturally, one seeks at least one solution.

The second condition is more nuanced. While many differential equations satisfying condition one can have numerous, often infinitely many, solutions, uniqueness is crucial for practical applications. For instance, the simplest ordinary differential equation illustrates this point:

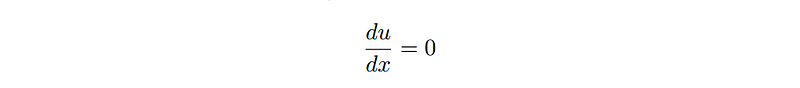
Anyone familiar with basic calculus recognizes that the solution to this equation is ( u = c ), where ( c ) represents any real number. This creates an uncountably infinite set of solutions, making it unhelpful in real-world scenarios. To ensure a unique solution, additional conditions, often termed boundary or initial conditions, must be introduced. For example, if we specify that ( u(0) = 3 ), we obtain a unique solution: ( u(x) = 3 ). While this is simple, establishing uniqueness becomes increasingly complex with higher-order derivatives or PDEs.

The third criterion is often the most challenging to demonstrate. If conditions one and two are met, then criterion three holds if small changes to the initial or boundary conditions only result in minor adjustments to the solution. The concept of “small” here aligns with mathematical notions of continuity and limits.

The earlier ODE example satisfies this criterion; the solution varies directly with the initial data. However, in chaotic systems, like the double pendulum, slight variations in initial conditions can lead to vastly different outcomes, illustrating how even simple equations can generate complex behaviors. This sensitivity is also evident in weather modeling, where minimal changes can drastically alter predicted outcomes, a phenomenon often referred to as the butterfly effect.

The implications of such uncertainty are significant. Individuals in hurricane-prone areas often experience forecasts that vary widely, underscoring the challenges in applied physics models where initial data is derived from empirical measurements that inherently contain errors. If all three criteria are met, prediction errors diminish in tandem with measurement errors. Without the third criterion, even minor inaccuracies in initial data can result in disproportionately large prediction errors, complicating the utility of having a unique solution.

The Role of Hadamard

The notion of well-posed problems was chiefly articulated by mathematician Jacques Hadamard (1865–1963), who extensively studied PDEs. He authored a pivotal text on this topic, where he defined the criteria for well-posedness. One of the earliest mentions of this concept appears in Hadamard's 1902 paper, which examined classical PDE problems and raised intriguing philosophical questions about their physical significance.

The paper begins with a quote from Henri Poincaré, known for his contributions across various mathematical and physical disciplines:

> "Physics does not only give us the occasion to solve problems…it makes us anticipate the solution."

This thought reflects the mutual support between pure mathematics and mathematical physics, where mathematical analogies often inspire physicists to discover new theories before they are experimentally validated, as seen in Maxwell’s electromagnetic theory and Einstein’s subsequent theories. This interplay suggests that physics not only benefits from mathematical formulations but also provides mathematicians with interesting challenges, particularly in determining boundary conditions for PDEs.

Hadamard distinguishes between two primary types of boundary conditions applied to PDEs: the Dirichlet condition, specifying values of the solution on the boundary, and the Cauchy problem, which provides conditions for both the function and one of its first partial derivatives. He posits that the well-posed problem typically aligns with a physical scenario.

For example, the Laplace equation, which is foundational in mathematical physics, can be expressed in three-dimensional space as follows:

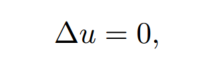
The Laplace equation serves as a fundamental example across various fields, from gravitation to electromagnetism. Hadamard analyzes this equation in a “half-space” domain, showing that while the Dirichlet problem remains well-posed, the Cauchy problem often is not, highlighting that not all formulations yield meaningful physical solutions.

Hadamard's analysis extends to the wave equation, which models wave propagation in three-dimensional space over time:

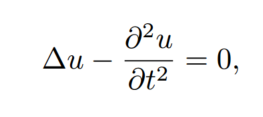
Here, the Cauchy problem is well-posed, allowing for unique solutions based on initial conditions, unlike the Dirichlet problem, which does not necessarily yield a well-posed solution.

However, Hadamard notes a key difference: while the Laplace equation maintains symmetry among its variables, the wave equation does not, raising questions about the well-posedness of Cauchy problems under certain boundary conditions. Hadamard proves that while a solution must be unique if it exists, it does not exist for specific conditions, further complicating the landscape of well-posedness.

Philosophical Considerations

Hadamard's insights lead to deeper philosophical inquiries. Why do well-posed problems align with physical scenarios while ill-posed ones do not? This inquiry echoes Wigner’s reflections on the applicability of mathematics in the physical world. Hadamard suggests that only those problems with natural physical relevance are constructively solvable, hinting at a profound relationship between mathematics and nature.

One possible explanation, offered by Richard Hamming, is evolutionary rather than metaphysical. Hamming theorized that our mathematical models evolved through natural selection, favoring those minds that could create models reflecting natural phenomena. This perspective suggests that our mathematics, rather than being absolute, is merely a product of specific evolutionary conditions.

Alternatively, it is plausible that our models simply reflect the complexities of the physical world, often serving as approximations of far more intricate realities. Numerous inverse problems—like deducing the shape of a drum from its sound—illustrate the practical challenges of ill-posed problems, emphasizing the need for further exploration in this area.

Further Resources

For those interested in learning more about Hadamard, a comprehensive biography is highly recommended. Additionally, during 2020, I created a series of video lectures introducing differential equations and their applications, which may serve as useful supplementary material:

1. An Introduction to PDEs
2. Boundary Value Problems
3. The Laplace Equation
4. The Wave Equation

References

• Hadamard, J. (1923). Lectures on Cauchy’s Problem in Linear Partial Differential Equations. Yale University Press.
• Hadamard, J. (1902). Princeton University Bulletin, 14(4): 49.
• Hamming, R. (1980). The American Mathematical Monthly, 87(2).
• Hertz, H. (1882). On the Contact of Rigid Elastic Solids and on Hardness. Chapter 6. Assorted Papers by H. Hertz.
• Lamb, H. (1932). Hydrodynamics. Cambridge University Press.
• Mazya, V. & Shaposhnikova, T. (1999). Jacques Hadamard, A Universal Mathematician. American Mathematical Society, London Mathematical Society.
• Mindlin, R. (1949). Journal of Applied Mechanics, 16: 259.
• Poincare, H. (1897). Congres International des Mathematiciens. Zurich.
• Poincare, H. (2001). The Value of Science: Essential Writings of Henri Poincare. The Modern Library, New York.
• Wigner, E. (1960). Communications on Pure and Applied Mathematics, 13(1).