Section 1.1: Practical Implementation of Shapley Values

In this tutorial, we'll leverage the classic Iris data set, closely following the original SHAP linear regression tutorial.

Before we begin, install the necessary libraries:

pip install pandas

pip install sklearn

pip install shap

pip install interpret

Next, load the required libraries:

import pandas as pd

from sklearn import datasets

import sklearn

import shap

import interpret.glassbox

Now, we will load the Iris data set into a format suitable for Scikit-Learn. If you're more accustomed to R, in this context, X represents your training data, while y is your label. Specifically, X1 denotes your training data, X2 your test data, y1 your training label, and y2 your test label.

Given that the Iris data set loads as an array, we need to convert it into a Pandas DataFrame, and the labels can be accessed using .target.

iris = datasets.load_iris()

X = pd.DataFrame(data=iris.data, columns=iris.feature_names)

y = iris.target

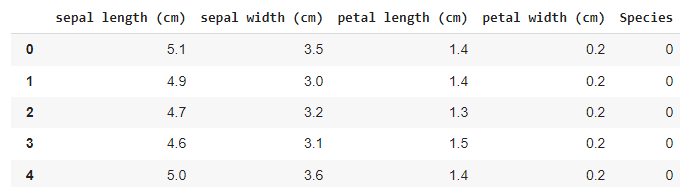
To ensure we have the correct data set, we can create a complete DataFrame that includes the label:

df = X

df['Species'] = y

df

Next, we will train our linear regression model:

model = sklearn.linear_model.LinearRegression()

model.fit(X, y)

Now, let's utilize SHAP to explain our model. Here’s a brief overview of the process:

• The variable X100 is used to create a background distribution by rearranging the original order of the data set.
• The Explainer function evaluates the average model outputs.

X100 = shap.utils.sample(X, 100)

explainer = shap.Explainer(model.predict, X100)

shap_values = explainer(X)

We can visualize the Shapley values with a waterfall chart:

shap.plots.waterfall(shap_values[0], max_display=20)

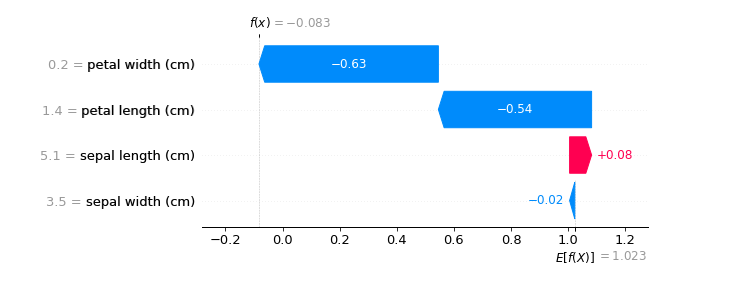
This chart illustrates the cumulative impact of each variable on the model's predictions. Essentially, each variable contributes a specific Shapley value for each row. By aggregating these values, you can gauge a variable's overall influence on the model. For instance, sepal length might positively impact the predictions, while petal width, length, and sepal width may have a more negative influence.

It's important not to take these Shapley values at face value. You must delve deeper into the data. Let’s further analyze the additive Shapley graph above.

In the subsequent analysis, we will switch from a linear regression model to a boosted tree model, clarifying how the additive graph appears when broken down into individual Shapley values.

model_ebm = interpret.glassbox.ExplainableBoostingRegressor()

model_ebm.fit(X, y)

explainer_ebm = shap.Explainer(model_ebm.predict, X100)

shap_values_ebm = explainer_ebm(X)

shap.plots.beeswarm(shap_values_ebm, max_display=5)

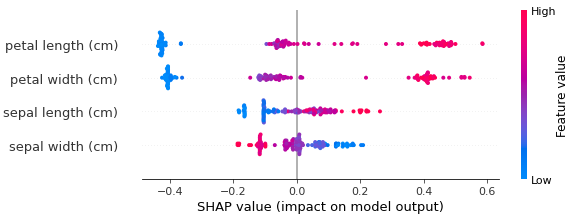
As seen here, petal width demonstrates some values with a positive impact, but the predominant negative influence stems from clustering around -0.4.

In conclusion, Shapley values should not be accepted without scrutiny. Their primary function is to aid in exploratory data analysis, providing a solid foundation rather than definitive answers.

Personal Reflection: How Shapley Values Enhance My Work

In my experience, Shapley values prove to be invaluable, especially when dealing with large, unfamiliar data sets. They offer more insightful starting points compared to automated insights generated by tools like PowerBI. Personally, I find greater value in understanding the additive effects of each variable rather than relying on random correlations.

Keep in mind that while a straightforward analysis might take only 10 minutes with a simple data set, more intricate data involving feature engineering or complex models could require additional time. In such cases, simplifying the data can facilitate a quicker analysis.

Enjoy exploring Shapley values!