Unlocking the Mystery of X: An Engaging Algebra Puzzle
Written on
Chapter 1: Introduction to the Puzzle
In this intriguing math challenge, we see that 10 = 10¹, 100 = 10², and 1000 = 10³. This serves as a crucial hint to tackle the equation at hand!
Can you utilize this hint to solve the problem? Feel free to pause reading, grab some paper, and give it a try. Once you're ready, continue for the solution!
Section 1.1: Understanding the Key Hint
The essence of this challenge lies in transforming 100 and 1000 into powers of 10, allowing us to simplify the equation into a cubic form.
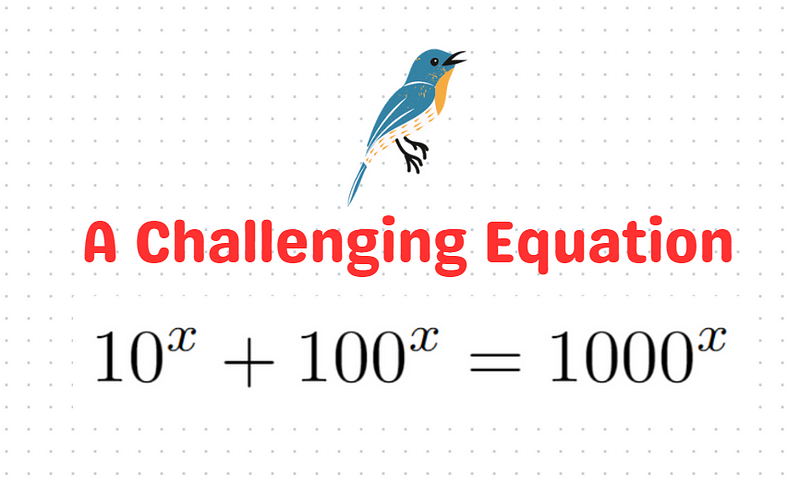
Next, we define y = 10^x, leading us to the following expression.
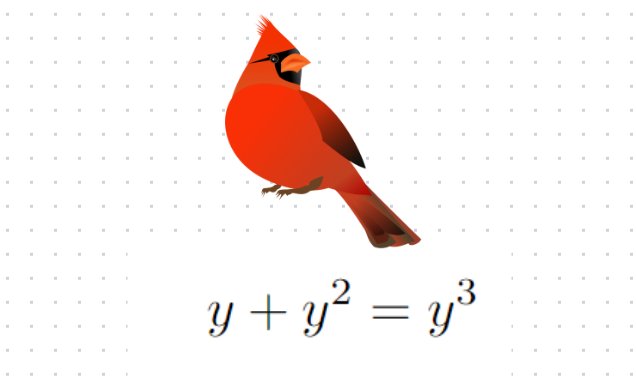
From here, we can consolidate everything on one side and factor it accordingly.
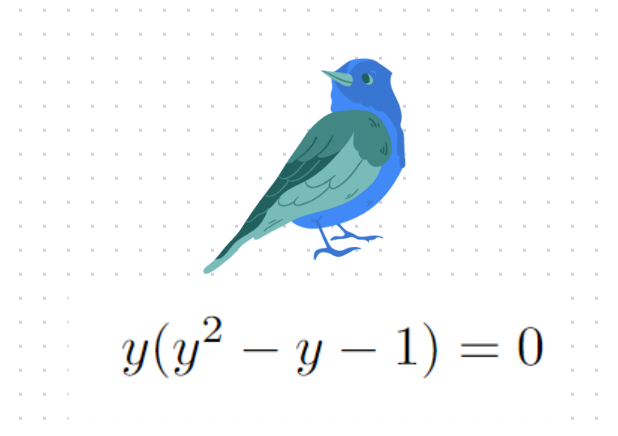
Upon inspection, we find that one solution for y is 0. However, since 10^x can never equal zero, we must explore another set of solutions. By applying the quadratic formula, we arrive at:
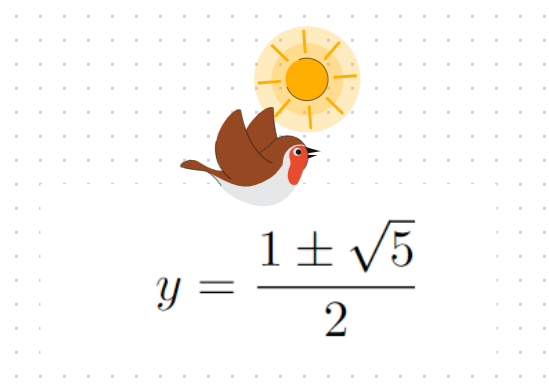
Thus, the solutions for x can be determined as follows:
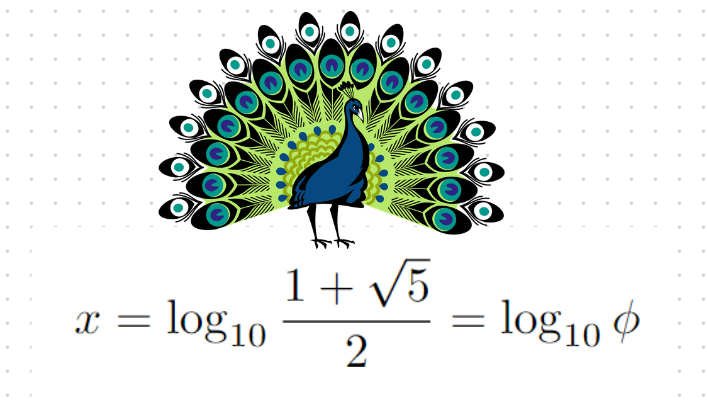
We disregard the negative solution as logarithms cannot be negative! This leads us to the golden ratio, which is our final answer.

What a fascinating process!
What were your thoughts as you worked through this? Please share in the comments—I’m eager to hear from you!
In this video, "How to Find X," you'll see a detailed breakdown of solving for x in various algebraic scenarios.
Chapter 2: Solving for X - Further Insights
The second video, "Solve for x in One Step (Simplifying Math)," provides additional methods and tips to simplify your approach to finding x.
Math Puzzles
The best math puzzles on Medium
Algebra, Geometry, Calculus, Number Theory, and more
Thank you for your engagement! If you enjoyed this puzzle, don't hesitate to clap for the article.

If you appreciate my writing, consider buying me a coffee! Your support means the world to me and helps in my academic journey.
With love, Bella 😊