Tree-Based Models in Machine Learning: Entropy, Gini Index, and Decision Trees
Written on
Chapter 1: Introduction to Tree-Based Models
In the sixth installment of our Machine Learning series, we delve deeper into tree-based models, a topic we previously introduced. These models are versatile and effective for solving both classification and regression challenges by systematically dividing data into branches.
This chapter will cover fundamental concepts such as entropy and the Gini index, along with a thorough explanation of decision trees, including their construction and application. Practical examples will illustrate how to use decision trees for classification and regression tasks.
Section 1.1: Decision Trees for Classification
A classification tree, given a labeled dataset, generates a series of conditional questions regarding specific features to determine labels. Unlike linear models, decision trees can effectively capture non-linear relationships between features and labels. Additionally, they do not necessitate that features share the same scale, such as through standardization.
When we refer to a classification tree, we are specifically discussing a decision tree designed for classification tasks.

For this analysis, we will utilize the "Wisconsin Breast Cancer Dataset," which can be directly imported into our project from the UC Irvine Machine Learning Repository, a common practice in various introductory resources on Artificial Intelligence.
To explore sample usage, click on this link and select the “Import In Python” button.
Section 1.2: Why Choose Decision Trees?
Decision trees are particularly advantageous when:
- You wish to capture non-linear relationships within your data.
- Model interpretability is crucial, and you want to visualize the decision-making process.
- You are dealing with categorical data and prefer not to convert it into numerical format.
- You want to emphasize important features by selecting them.
- You are tackling multiple classification problems, where decision trees may outperform logistic regression.
To illustrate their effectiveness, we can visually compare decision trees and logistic regression models.
Now, let’s construct a Logistic Regression model and visualize our comparison chart.
Section 1.3: The Learning Process of Decision Trees
First, let’s clarify some terminology. A decision tree is a data structure composed of nodes arranged hierarchically. Each node represents a question or prediction. The root node is where the tree begins and has no parent; it contains a question that leads to two child nodes through branches. Internal nodes have parents and also pose questions leading to child nodes. Leaf nodes, conversely, do not have any children and are where predictions occur. When trained on a labeled dataset, a classification tree learns patterns from the features, aiming to produce the purest leaves possible.
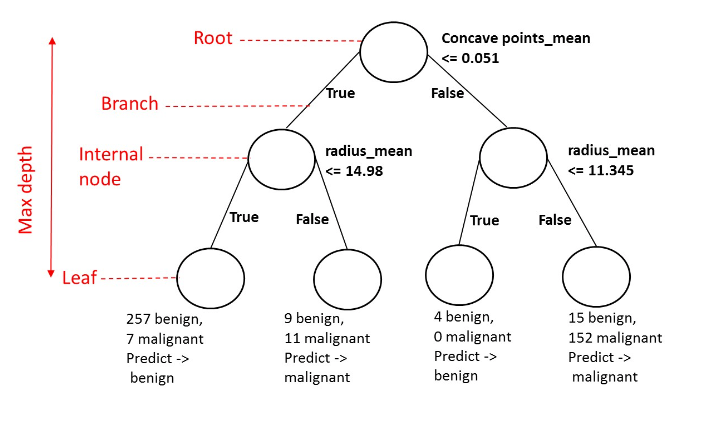
So, what mathematical principles guide the creation of these leaves? For regression trees, the purity of a node is evaluated using the mean squared error (MSE) of the target values within that node. The aim is to identify splits that generate leaves where target values closely align with the mean value of that leaf.
Section 1.4: Understanding Mean Square Error (MSE)
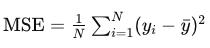
Here, N represents the total instances in the node, Yi is the actual target value of the i-th sample, and ȳ is the average target value across all samples in the node.
As the regression tree is developed, it seeks to minimize the MSE at each split, ensuring that the target values in the leaves are as close as possible to the average target value of that leaf.
Section 1.5: Total Purity Reduction Explained
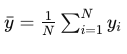
The regression tree algorithm strives to maximize the reduction in impurity (ΔMSE) at each split, utilizing Information Gain as the metric for assessing this purity reduction.
Chapter 2: Information Gain and Entropy
Information Gain quantifies the extent of uncertainty or impurity diminished by splitting a dataset based on a specific feature. This measurement is integral when constructing decision trees and selecting features at each split. The goal is to segment the dataset in a manner that maximizes Information Gain.
Entropy serves as a foundational concept here, representing the uncertainty or randomness within a dataset. High entropy indicates a more complex dataset, while low entropy suggests a more organized one.
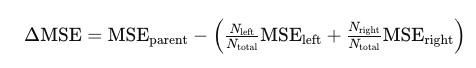
In this formula, H(D) denotes the entropy for dataset D, k is the number of classes, and p-i represents the probability of the i-th class.
Section 2.1: Calculating Information Gain
Information Gain measures the decrease in entropy when a dataset is partitioned based on a feature:
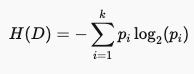
In this equation, IG(D, A) refers to the Information Gain of feature A for dataset D, H(D) is the entropy before splitting, and Values(A) is the set of possible values for feature A.
To summarize, entropy gauges uncertainty in a dataset, while Information Gain assesses the reduction in entropy achieved through data splitting. High Information Gain results in purer (less ambiguous) datasets, making it a preferred criterion for decision tree construction.
Section 2.2: Gini Index and Decision Trees for Regression
Similar principles apply to the Gini index and entropy when determining Information Gain. The choice of which criterion to use may depend on project specifics, such as dataset size or hyperparameters.
In regression tasks, the target variable is continuous, meaning the model output is a real number. Employing decision trees in this context can enhance model performance over linear regression.
We will demonstrate this with the Auto MPG dataset from the UC Irvine Machine Learning Repository.
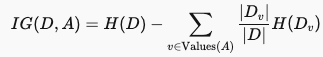
Our findings indicate that regression trees can provide a slight advantage over linear regression. Note that these results may vary based on dataset size and hyperparameters.
In conclusion, we have thoroughly examined decision trees. In the next chapter, we will discuss concepts such as Bias-Variance Tradeoff, Bagging, Random Forests, Boosting, and Model Tuning. Stay tuned for further articles!