Chapter 1: The Nature of Uncertainty in Neural Networks

Neural networks are inherently uncertain. When we input data into these models, the resulting output may not accurately reflect reality. To better grasp the nuances of this uncertainty, it's crucial to differentiate between two distinct forms:

1. Aleatoric Uncertainty: This type of uncertainty persists regardless of additional data.
2. Epistemic Uncertainty: This uncertainty diminishes with the inclusion of more data.

By categorizing uncertainty in this manner, we gain insights into the learning mechanisms of neural networks. Addressing these uncertainties requires different approaches, as will be discussed further on.

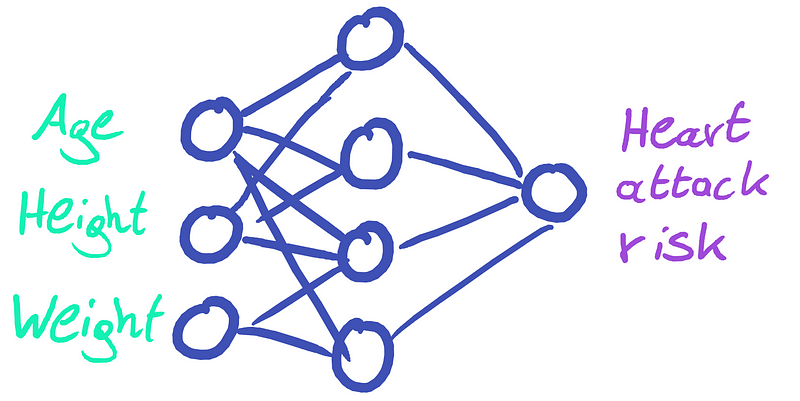
To illustrate the concept, consider a hypothetical scenario where we develop a medical application aimed at assessing heart attack risk for patients. The neural network takes various patient attributes—such as age, height, and weight—and generates an output percentage, for instance, 2%, indicating the likelihood of a heart attack within a decade.

Assuming we meticulously followed best practices—utilizing a robust dataset, partitioning it into training, validation, and testing sets, and experimenting with multiple architectures—we believe we have developed a reliable model for predicting heart attack risks.

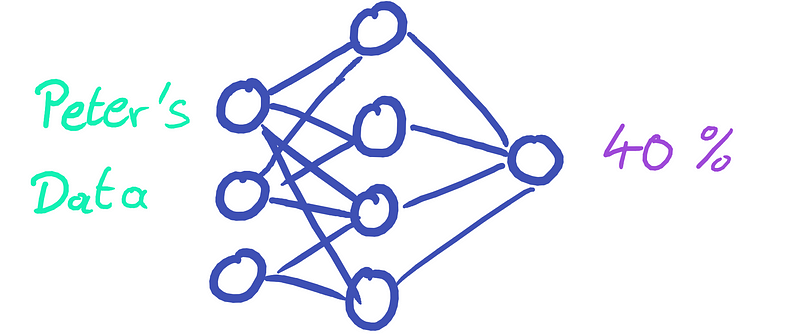
When Peter, a patient, provides his data, the neural network predicts a 40% risk of a heart attack. This alarming figure prompts Peter to question the certainty behind this prediction.

There are two potential sources of uncertainty in our prediction:

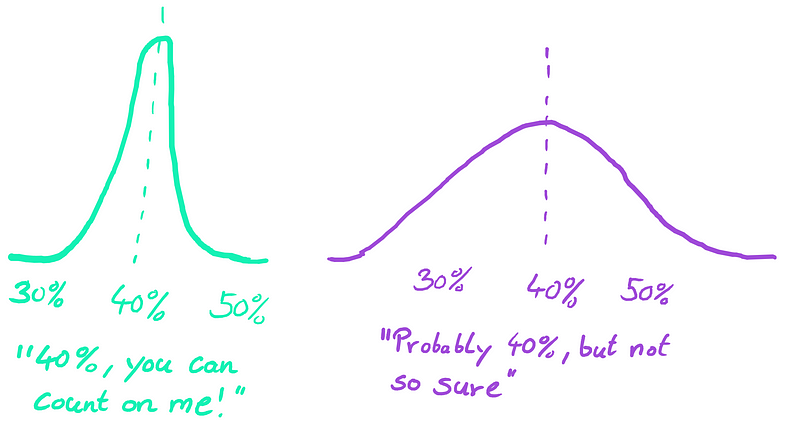
1. Individuals sharing Peter’s characteristics may exhibit vastly different heart attack risks. The network merely outputs an average risk, which could be better represented by a probability distribution. A wider distribution, or greater variance, indicates higher uncertainty—this is known as aleatoric uncertainty.

2. The second source of uncertainty arises if Peter’s profile is unique or poorly represented in the training data. Consequently, the network might be unfamiliar with such inputs and generates a 40% risk purely out of necessity, reflecting epistemic uncertainty.

Recognizing these two types of uncertainty does not provide clarity for Peter. The output remains a 40% risk, leaving us unable to determine whether the model is highly confident or completely lost.

So, how can we develop a neural network that communicates its level of certainty? Given the distinct nature of aleatoric and epistemic uncertainties, we need to address them using separate strategies.

Section 1.1: Tackling Aleatoric Uncertainty

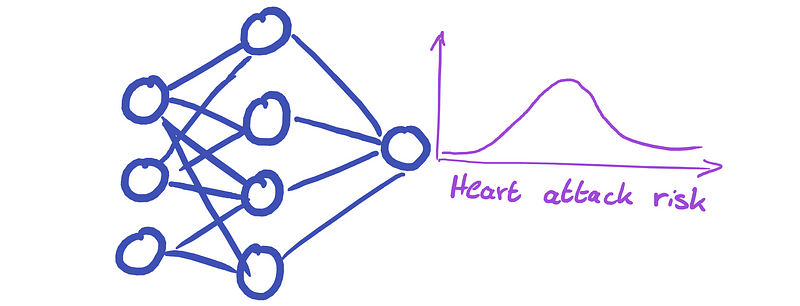
Aleatoric uncertainty is intrinsic to the data itself. No matter how much training data we collect, there will always be individuals with identical characteristics but differing risk levels. To better manage this uncertainty, we can modify the neural network to produce a probability distribution rather than a single prediction.

To accomplish this, we select a distribution type—such as the normal distribution N(µ, σ²)—which has two parameters: the mean (µ) and the variance (σ²). Instead of returning a single heart risk percentage, the network will output values for both the mean and the variance.

The loss function must also be adjusted to ensure that the outputs for µ and σ² maximize the likelihood of the observed training data. In essence, the network transitions from predicting just the mean (µ) to also estimating the variance (σ²)—the aleatoric uncertainty—based on the data.

A noteworthy aspect is that minimizing mean squared error (MSE) loss is equivalent to maximizing the likelihood concerning the distribution N(µ, 1), meaning the variance can be fixed at 1.

If you’re interested in experimenting with these concepts, TensorFlow offers a powerful extension called TensorFlow Probability, which simplifies the implementation of various distributions.

Returning to our uncertainties, while we’ve managed to have the neural network provide both the heart risk percentage and the associated uncertainty, what happens when data is scarce? If Peter’s profile is indeed rare, the model may yield arbitrary risk percentages and variances, indicating its lack of knowledge. This illustrates why aleatoric and epistemic uncertainties are independent and necessitate separate handling.

Section 1.2: Addressing Epistemic Uncertainty

Epistemic uncertainty stems from incomplete information and the unavailability of all relevant data. In real-world situations, achieving a complete dataset is often unattainable, leaving some degree of epistemic uncertainty. However, as more data becomes available, this uncertainty can diminish.

Let’s take a moment to consider how to model the current epistemic uncertainty of our neural network. What are we uncertain about, and how would additional data affect our model? The answer lies in the weights of the network. With more data, these weights would adjust, and our uncertainty lies in not having fixed weights but rather probability distributions for them.

This concept is the foundation of Bayesian neural networks (BNNs), which treat weights as probability distributions rather than fixed values.

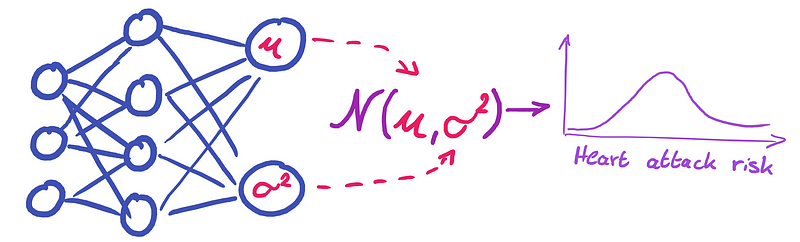
BNNs update these weight distributions using Bayesian inference, allowing us to quantify our epistemic uncertainty alongside the network’s predictions. While they may require more computational resources for training, they provide an additional output indicating the level of epistemic uncertainty.

TensorFlow Probability also supports Bayesian neural networks if you're keen to explore this avenue.

Conclusion

The outputs of neural networks are always accompanied by uncertainty, which can arise from either data variance (aleatoric uncertainty) or from incomplete datasets (epistemic uncertainty). Both types of uncertainty can be addressed and quantified through distinct methodologies.

In high-stakes applications, such as medical predictions like Peter's heart attack risk, understanding the level of uncertainty is crucial. Implementing probabilistic deep learning techniques can enhance the safety and reliability of neural networks in life-critical situations.

If you have any questions or comments, feel free to connect with me on LinkedIn. For those interested in further insights, consider subscribing to my newsletter at marcelmoos.com/newsletter. For deeper exploration into probabilistic deep learning, check out these resources:

• Regression with Probabilistic Layers in TensorFlow Probability — TensorFlow Blog
• What My Deep Model Doesn’t Know… — Yarin Gal

Chapter 2: Deepening Understanding of Uncertainty

This video from MIT discusses the intricacies of uncertainty in deep learning, providing valuable insights into how we can better understand and manage these uncertainties.

In this video, learn practical strategies for addressing uncertainty in deep learning, focusing on techniques that enhance model reliability and accuracy.