Harnessing AI to Revolutionize Quantum Mechanics Computation
Written on
Chapter 1: The Challenge of Quantum Mechanics
The intricate task of computing quantum mechanical properties, such as the atomization energy of compounds, can be a time-consuming endeavor, often requiring hours to weeks with conventional methods. This article delves into the innovative application of deep neural networks (DNNs) to accomplish these calculations in just seconds, achieving an impressive accuracy rate of 99.8%.
A notable quote from Nobel Laureate Paul Dirac highlights the complexity of quantum mechanics:
“The underlying physical laws necessary for the mathematical theory of a large part of physics and the whole of chemistry are thus completely known, and the difficulty is only that the exact application of these laws leads to equations much too complicated to be soluble. It therefore becomes desirable that approximate practical methods of applying quantum mechanics should be developed, which can lead to an explanation of the main features of complex atomic systems without too much computation.” — Paul Dirac, 1929
Section 1.1: Traditional Approaches to Quantum Mechanics
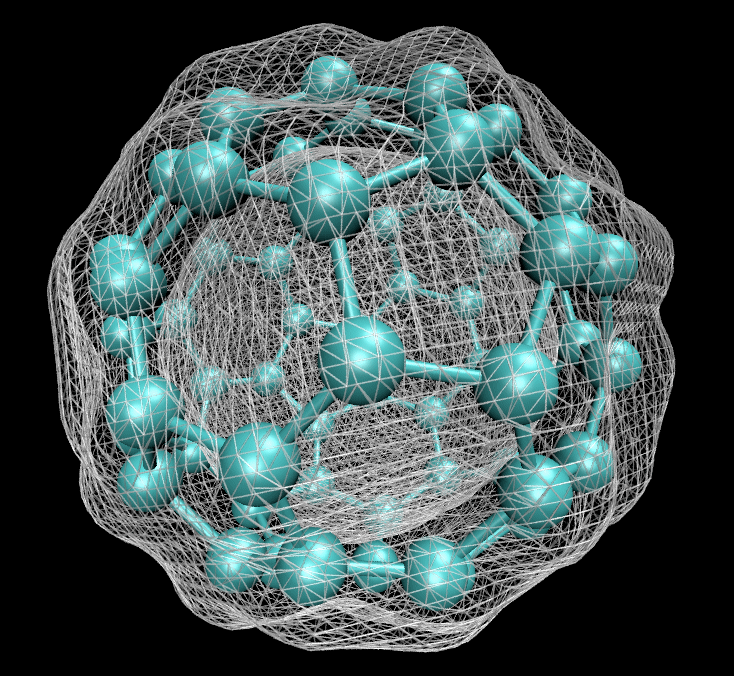
The development of approximate methods to tackle the complexities of quantum mechanics led to the emergence of two primary techniques: Hartree-Fock Theory (HF) and Density Functional Theory (DFT). The latter has seen significant advancements since the 1990s and remains a fundamental tool in computational chemistry and materials science. For instance, DFT can be utilized to accurately depict the electron density surface of large molecules like buckminsterfullerene:
However, despite its efficacy, DFT and HF can still be time-intensive, often taking hours, days, or even weeks to yield results. By harnessing the capabilities of deep neural networks, we aim to significantly shorten this timeframe to mere seconds.
A Google Colab notebook accompanies this article for those interested in a deeper exploration of the methodologies discussed herein. Credit is due to G. Montavon et al. for their pioneering work in this area, which continues to inspire further research.
Section 1.2: Understanding the Coulomb Matrix
- What is the Coulomb Matrix and Why is it Essential?
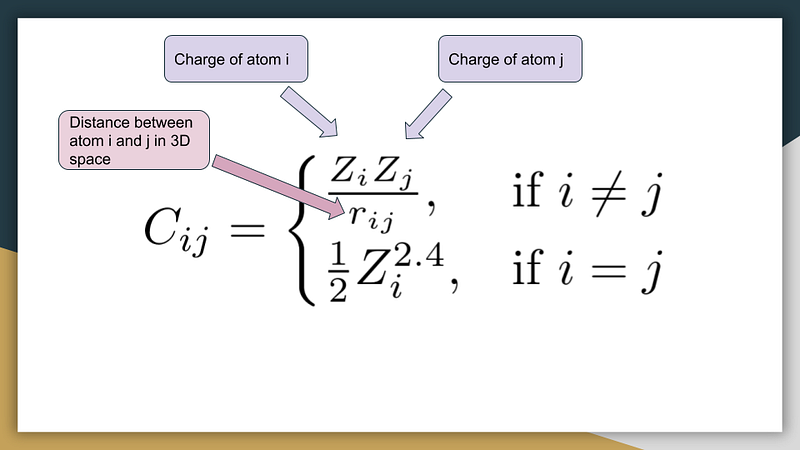
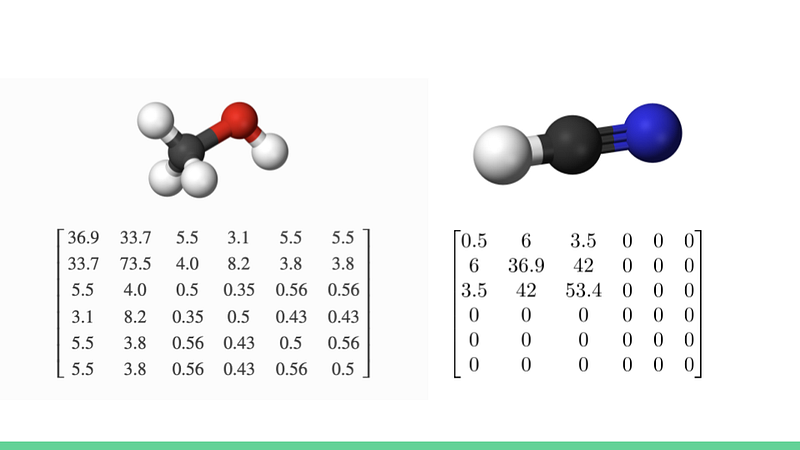
The Coulomb Matrix serves as a crucial tool in capturing the interactions of various atoms within a molecule. It effectively stores the pairwise electrostatic potential energy for each atomic pair, factoring in the charge associated with each atom and their respective 3D spatial coordinates.
The Coulomb Matrix is defined as follows:
Utilizing the Coulomb Matrix as input data is advantageous due to its predictive capabilities. With it, one can perform DFT or HF calculations to derive complex quantum mechanical properties. Essentially, we leverage the Coulomb Matrix to implicitly educate our machine learning model about the principles of quantum mechanics.
- Challenges Associated with the Coulomb Matrix
While the Coulomb Matrix is invaluable, it does present three main challenges, all of which can be addressed to create an effective model.
2.1 Molecule Size Variability: Different molecules yield differently sized Coulomb Matrices, which can complicate machine learning applications. This issue can be mitigated by padding the matrices of smaller molecules.
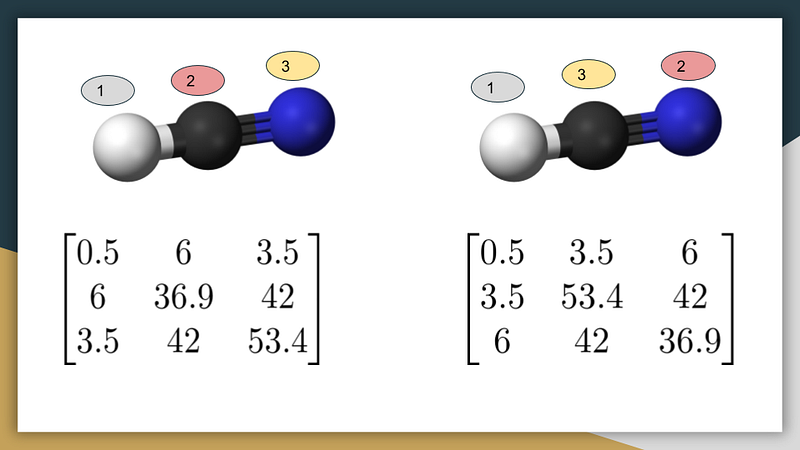
2.2 Labeling Variability: There are multiple ways to label a molecule, leading to distinct Coulomb Matrices for the same compound. We can resolve this by sorting the matrices based on the largest atoms, albeit with an introduction of slight noise to enhance the neural network's robustness and prevent overfitting.
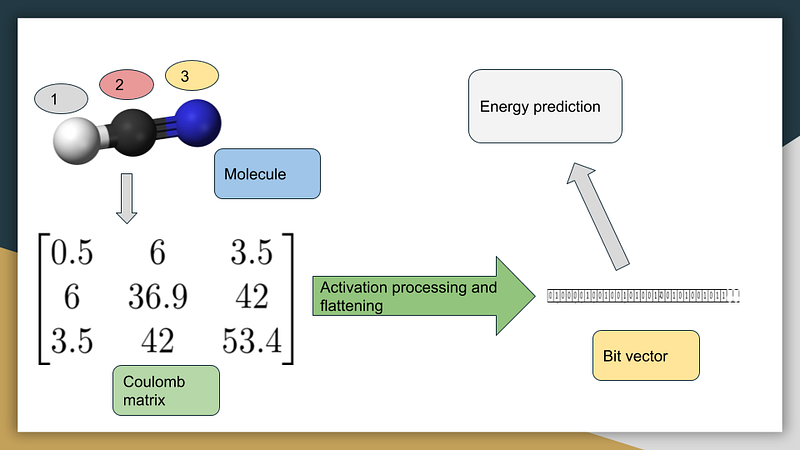
2.3 Information Loss in Ordering: To maintain critical labeling information, we can transform the Coulomb Matrix into a binary format by applying an activation function. This transformation allows us to retain the essential data while enabling effective machine learning processes.
Chapter 2: Data and Neural Network Architecture
- Data Utilization
Our dataset comprises approximately 7,000 molecules, each exhibiting various functional groups. For every molecule, we calculate the Coulomb Matrix and determine its atomization energy using DFT. This energy measurement serves as the target variable for our neural network training.
- Neural Network Framework
The architecture of our deep neural network is straightforward, consisting of two fully connected hidden layers with 400 and 100 neurons, respectively. We initialize the weights using Xavier Initialization. While there is ample opportunity for more intricate architectures, this basic configuration effectively addresses our specific problem.
We employ the Adam optimizer to minimize the mean squared error (MSE) loss function, with the implementation carried out using Google’s TensorFlow library. The complete code can be found in the accompanying Colab notebook.
- Results and Future Directions
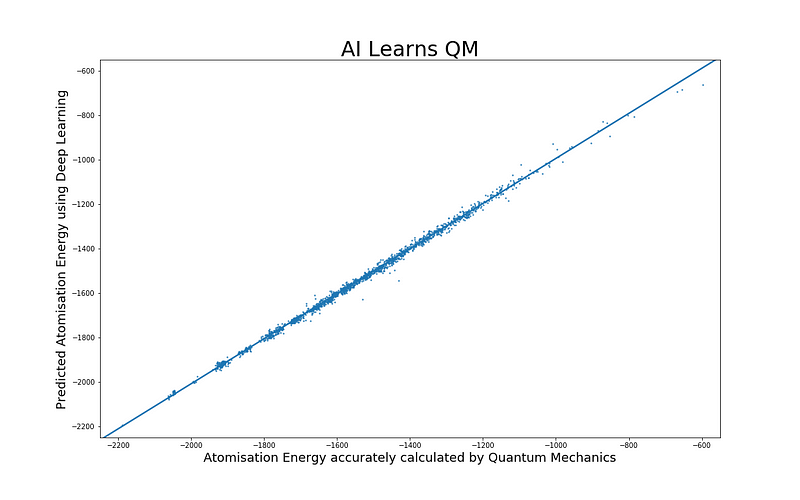
For those interested in a more detailed investigation, the Google Colab notebook is available for exploration. Users can run the code seamlessly, thanks to Google Colab's free GPU support. The regression results indicate a strong performance, as illustrated below.
As the straight line represents ideal predictions, the scattered points reflect the outcomes generated by the DNN.
- Next Steps
To delve deeper into the concepts discussed in this article, readers are encouraged to refer to the original research paper. The research team has published additional papers that further expand on this topic, which are worth exploring.
If you found this article insightful, feel free to engage with me on LinkedIn and share your thoughts. Looking forward to our next discussion!
Explore the implications of AI in unifying general relativity and quantum mechanics in this insightful discussion featuring Tyler Cowen.
Demis Hassabis and Lex Fridman discuss whether AI can unravel the complexities of quantum mechanics in this thought-provoking conversation.