Understanding the Basics

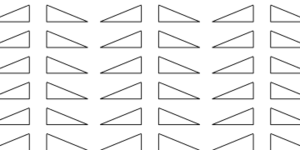
To kick off our discussion, let’s begin with the simplest tiling pattern, referred to as p1. This pattern is as straightforward as it gets; there are no rotations or reflections involved. The same image is simply repeated throughout. This pattern is frequently employed in wallpaper design, as it can be visually appealing when the right image is chosen. Any shape or parallelogram can serve as the repeated tile.

This tiling pattern is known as a translation, which involves taking one image and shifting it to another location. To create this tile design, the floral image is simply translated across multiple positions. All types of wallpaper incorporate translation, but p1 is unique in that it solely consists of translation without any additional transformations. You'll likely encounter translations in various artworks, as it merely involves copying an image and relocating it. However, we can explore some more intricate patterns now.

Let’s take a look at another fundamental wallpaper type. The next type, pm, is similar to p1, but incorporates a mirror effect in each column. Here, we have sets of images that feature their reflections aligned side by side. A reflection mirrors an image, but it also involves flipping it. This wallpaper type can often be mistaken for p1, but a crucial difference exists. In the above illustration, the stars are created by two objects that are mirror images of one another. The star is not the primary object; instead, half of the star serves as the basic element. Visualize a vertical line splitting the star from top to bottom, creating the symmetry. This is not the case for the floral example in p1.

The axis of symmetry in p1 does not have to be vertical; sometimes, a wallpaper of this type may exhibit a horizontal or even diagonal axis. This variability can make identifying p1 challenging as it can resemble other types. The key is to look for a line of symmetry. Any object can possess a line of symmetry. Try to spot a reflective example in your surroundings—most computer mice display near-symmetrical designs.

Introducing a New Dimension

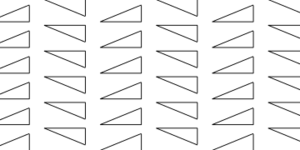
Next, I will introduce a concept known as glide reflection. This is akin to a regular reflection but involves reflecting the entire axis simultaneously. The group that consists solely of glide reflections is labeled pg. In the example above, the black arrows indicate the upward and downward directions of the columns. Each direction corresponds to a distinct column of the translation. The basic object here features a stack of alternating black and yellow arrows.

You might anticipate the next type. We are now going to merge a reflection with a glide reflection to create the wallpaper type cm. What distinguishes cm is that the axes of both reflections align on the same axis. Glide reflections can occur vertically, horizontally, and diagonally, just like basic reflections.

Similar to the earlier pm example, we employ a mirror effect to create individual stars. However, the rows are now offset from one another. We reflect each object along a vertical line, and some objects are reflected again, resulting in staggered rows of mirrored shapes, akin to the stars depicted above. Notice how these stars mirror the structure of the simplified version below. Hint: each star is formed by two triangles.

If you're still seeking clarity, remember that the fundamental object here is half of a star.

The Concept of Rotation

If you have any familiarity with geometry, you may notice that we are missing a critical action known as rotation. As the name suggests, this involves taking an image and spinning it by a certain angle. The example above, p2, features a 180° rotation for its basic shape. This is where wallpaper types can quickly become complex! Challenge yourself to identify the rotation in the image above and determine what the basic object is.

While I won’t discuss all the remaining types involving rotation, that would be lengthy and tedious. However, I will highlight a few more intriguing patterns. The p3 wallpaper type is one of my personal favorites. If you disregard the colors, the tiling from Alhambra at the beginning of this article corresponds to type p3. It includes three rotations at 120° with no reflections. Can you identify the basic object in that illustration?

What happens if we combine all our techniques: translation, reflection, glide reflection, and rotation? This opens up numerous possibilities, including the wallpaper type p6m, which yields stunning hexagonal designs.

I hope this overview provides insight into the captivating nature of wallpaper types! There are many more that I haven’t covered, with most combining all forms of transformations we’ve explored. For now, let's see how these patterns inspired one of history's most fascinating artists: M.C. Escher.

The Mathematical Influence

If you’ve encountered M.C. Escher's work, you might recognize how these wallpaper types influenced him. He visited the Moorish temple illustrated at the start of this article and meticulously copied its patterns into his notebook. During this time, he expressed:

> "It remains an extremely absorbing activity, a real mania to which I have become addicted, and from which I sometimes find it hard to tear myself away." > > — M.C. Escher

This obsession is evident in his artwork. Below is a stunning example of p4g.

Escher devoted many years to exploring tessellations and produced numerous masterpieces. I highly recommend searching for his name to discover the incredible tilings he created. A fun exercise is to select one of his works and identify which of the 17 wallpaper types it represents. It’s surprisingly challenging!

Escher remained relatively unknown until the age of 70, when he held his first exhibition. Since then, he has gained immense popularity, and his art has been utilized to illustrate complex mathematical concepts; wallpaper types are just one of the themes he explored. Remarkably, he had no formal mathematical training. I’ll leave you with a thought-provoking quote that may shed light on his source of inspiration.

> "I don’t use drugs, my dreams are frightening enough." > > — M.C. Escher

Further Exploration

I hope you found this informative! Wallpaper types are fascinating as they exemplify how mathematics permeates various aspects of life. I couldn't cover the entire theory in this article, but if you wish to explore further, I have included several resources below for your reading pleasure.

• The Wikipedia page on this topic is exceptional and served as a key inspiration for this article. It’s a fantastic starting point for more advanced discussions about wallpaper, complete with intriguing mathematical notation.
• Another major influence for this article came from the Math and the Art of M.C. Escher website, which is packed with interesting information connecting Escher and mathematics in an accessible manner. Be sure to check it out!
• This formal mathematical paper provides much of the theoretical background discussed here. While it may be more challenging to comprehend, it’s rewarding for those willing to delve deeper.
• The EscherSketch website allows you to create your own wallpaper using each of the 17 types.
• For a captivating biography of M.C. Escher and his works, I recommend The Magic Mirror of M.C. Escher.

Additionally, I have other articles that you might find interesting—feel free to explore them!

If you enjoyed this piece, consider showing your appreciation! You may also want to follow me for more articles like this or subscribe to my email list. I publish weekly content related to math and science.