Section 1.1: The Rationale for Subtracting with Addition

Historically, before advanced technology became commonplace, complex calculations were accomplished using mechanical devices. Inventors and manufacturers optimized these machines by creating algorithms that utilized only addition, resulting in smaller and more cost-effective tools.

Even in today's digital age, where transistors function as binary switches, algorithms that allow subtraction through addition continue to promote efficiency and compactness in computational devices. Hence, this method remains prevalent in modern technology.

Discover how to subtract by adding in this detailed video.

Section 1.2: A Practical Example of Subtraction Using Addition

To illustrate this concept, let’s consider the subtraction of 25689 and 12865. Typically, we would perform the operation as shown below:

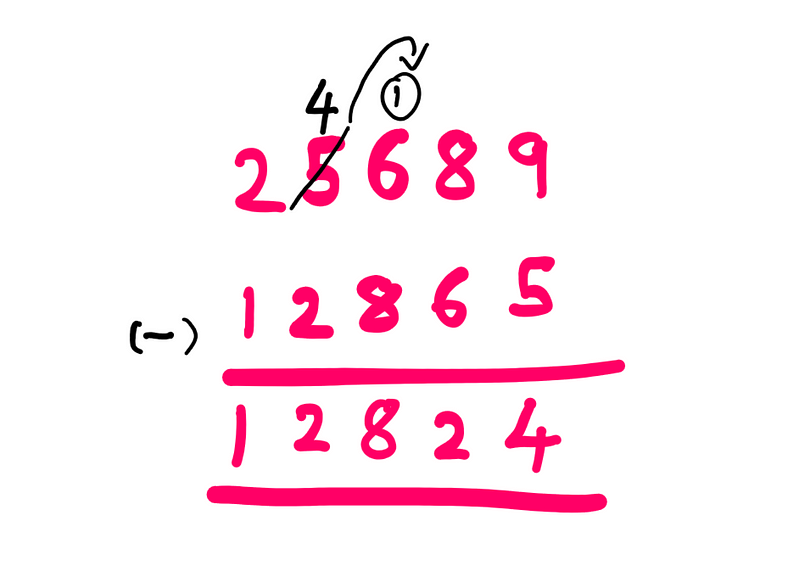
However, there is a way to achieve the same result through addition:

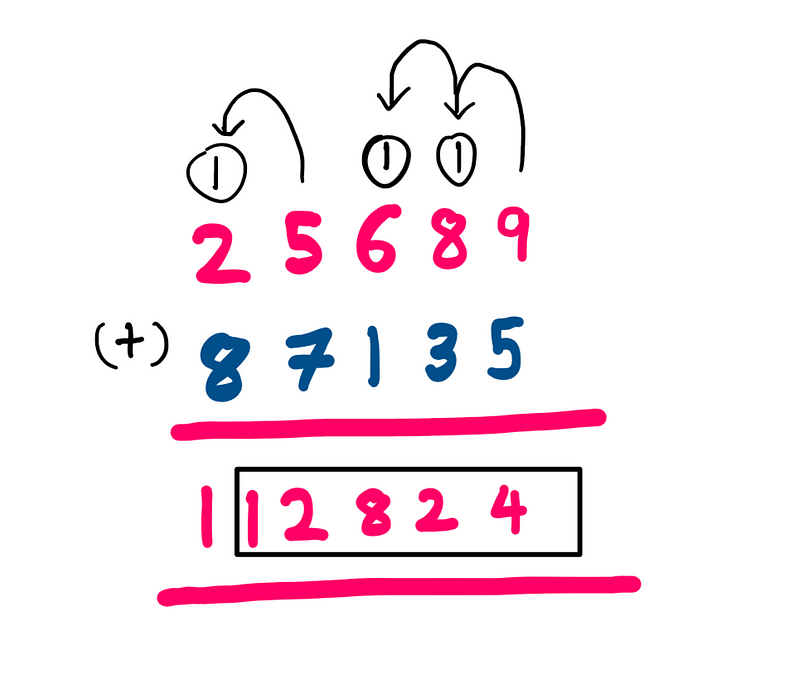
This method raises some immediate questions. How did I determine which number to add to 25689? And why did I ignore the leftmost ‘1’ in the addition result? Let’s delve into the algorithm used to answer these queries.

Subsection 1.2.1: The Algorithm Behind Subtraction via Addition

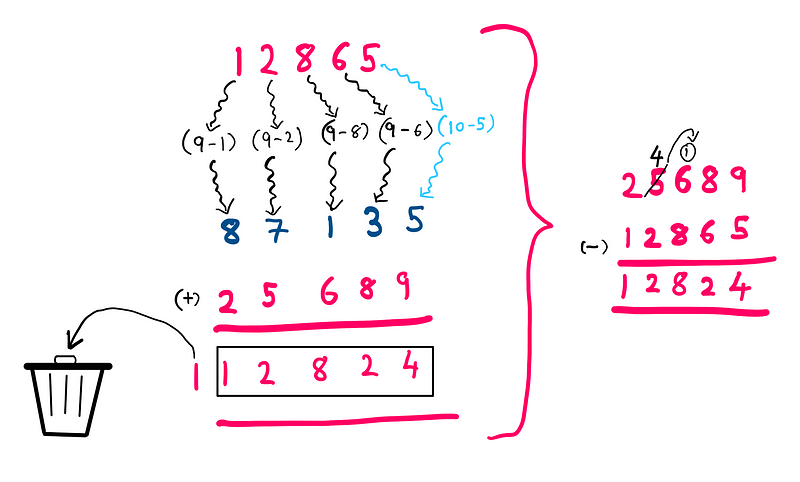
To break down the process, we identify the minuend (the number from which we subtract) and the subtrahend (the number being subtracted). In essence, we replace the subtrahend with an addend. The algorithm involves subtracting each digit of the subtrahend from ‘9’ (except for the last digit), and then subtracting the last digit from ‘10’. This provides the necessary addend. Finally, we disregard the first digit of the sum to arrive at the subtraction result.

If this explanation seems convoluted, the mathematical illustration below should clarify:

To reinforce this concept, here are additional examples demonstrating the same algorithm:

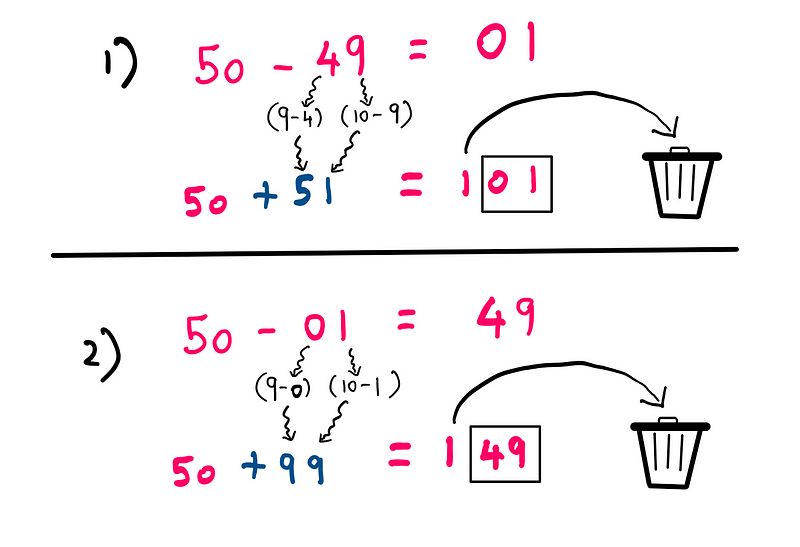
Section 1.3: Understanding the Method of Complements

The algorithm is based on a principle known as the method of complements. This mathematical framework relies on two key ideas:

1. Subtraction can be represented as the addition of a negative value, such as (5–3) = 5 + (-3).
2. In any base system, including our decimal example, we can pre-encode the additive inversion for each digit.

In the previous example, we compute the nine's complement for the subtrahend’s digits, except for the last digit, for which we calculate the ten’s complement. The addition process yields a result that exceeds the required significance level, with the excess digit being discarded.

Section 1.4: Expanding to Modern Computational Systems

As mentioned earlier, modern computers also utilize addition for subtraction. Digital computers rely on similar principles, with the difference being that they compute the two’s complement instead of the nine’s complement.

The algorithm explored in this article is just one method to subtract using addition; numerous algorithms exist, with generalization achieved through a concept called Radix Complement.

In conclusion, while subtracting through addition may seem perplexing for manual calculations, it is a standard practice in automated computation, offering a resource-efficient solution.

Learn about the Add to Subtract strategy in this engaging video.

Credit: Some illustrations in this article were inspired by Henry Reich's work.

I hope this article has provided you with valuable insights. If you enjoyed it, consider showing your support by clapping, following, and subscribing.

For further reading, you might be interested in: How Much String Would You Need To Wrap The Earth? and How To Hear Acceleration Without Modern Technology.

You can read the original essay here.