Bootstrapping: A Solution

Bootstrapping comes to our aid! This method generates a finite number of samples, computes a summary statistic (like the mean) for each sample, and establishes an interval for the solution. Previously, collecting 10,000 samples seemed daunting, but with Python, we can make it manageable.

In addition to forming confidence intervals, bootstrapping can also facilitate significance tests. This article aims to clarify bootstrapping and its role in generating confidence intervals.

Why Choose Bootstrapping?

If your supervisor questions the use of bootstrapping, you can explain that it is a non-parametric method. This means it does not rely on any assumptions about the underlying data distribution. Therefore, we don't need to contend with issues of data normality or equal variance. Unlike traditional t-tests, bootstrapping doesn't require strict assumptions, although a representative sample size is essential.

Understanding Bootstrapping

Bootstrapping involves using resampled data (with replacement) to carry out statistical inference. A simple example in Python illustrates this concept effectively:

import numpy as np

reel_views = [191, 145]

bootstrapped_video_views = np.random.choice(reel_views, size=len(reel_views))

print(f'The first sample: {bootstrapped_video_views}')

In this example, the code might return samples like [191, 191], [145, 145], or [191, 145]. The process of random selection and replacement helps us understand bootstrapping better.

Generating Bootstrapped Confidence Intervals

We can estimate uncertainty through bootstrapping by calculating confidence intervals. The goal is to identify an interval for the summary statistic (mean) that encompasses the true mean of the sample population. The procedure is as follows:

1. Create a bootstrap sample by randomly selecting with replacement from our data (video views).
2. Calculate the summary statistic (mean) from this new sample and store it as a bootstrap replicate.
3. Repeat these steps a fixed number of times (typically 10,000).
4. Determine the 2.5 and 97.5 percentiles from the stored summary statistics.

Here's how the code looks:

def draw_bs_reps(data: list, func: Callable, size: int = 10000) -> np.array:

"""

Generate bootstrap replicates. Typical size = 5,000 - 10,000 repetitions.

"""

rng = np.random.default_rng(seed=42)

bs_sample = rng.choice(data, size=(size, len(data)))

bs_replicates = np.apply_along_axis(func, arr=bs_sample, axis=1)

return bs_replicates

reel_views = [191, 145, 198, 192, 1022, ...] # Large Representative Sample

bootstrap_replicates = draw_bs_reps(reel_views, np.mean)

conf_int = np.percentile(bootstrap_replicates, [2.5, 97.5])

print(f'95% Confidence Interval: {conf_int}')

For example, the output might show a 95% confidence interval of [137.9, 150.3]. This implies that if we were to repeatedly sample the views from top brands, 95% of the sample means would fall between these two values.

Visualizing Results

Visual representation of the results can enhance understanding. When generating bootstrap replicates, consider using ECDFs, KDE plots, or histograms. Personally, I find ECDFs and KDE plots superior since they display all data points without binning. Below is a KDE showing all 10,000 bootstrap replicates:

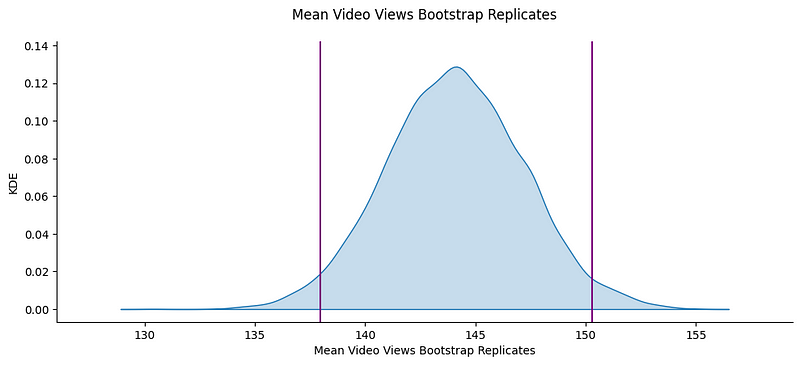
The purple lines indicate that 95% of the bootstrap mean replicates fall within these bounds. If the interval appears wide, increasing the number of bootstrap replicates (e.g., to 20,000) won’t necessarily narrow it. To achieve a tighter interval, you’ll need to collect a larger dataset.

Key Insights

• Bootstrapped confidence intervals assist in estimating uncertainty.
• This technique requires a large and representative sample.
• Bootstraps cannot magically increase the data within a sample.
• To obtain narrower intervals, you must enhance your sample size.

In the upcoming article in this bootstrapping series, I will explore significance tests. Thank you for reading!